6.1. Analysing proportions

The binomial test

Bárbara D. Bitarello

2025-11-12

Key learning goals

• Explain probabilities and proportions. Which is the parameter? Which is the estimate?
• Explain the binomial. When would you use it?
• Understand the binomial distribution and connect it to simple probability rules.
• Quantify the expected mean and variability of a binomial distribution.
• Be able to appropriately conduct and interpret a binomial test.

Proportions

• A proportion is the fraction of individuals having a particular attribute. i.e. # successes divided by # trials

• A proportion is also the probability that any an individual randomly sampled from that population will have that attribute

Example: Murphy’s Law

Researchers found that 6101 of the 9821 slices of toast thrown in the air landed butter side down. What proportion of the slices landed butter side down? Is the deck stacked against us?

How would you test this?

From proportions to the binomial

Let’s use this estimated proportion as our best estimate for the true probability of landing butter side down. To make the math a little easier, let’s assume that the true probability that toast falls butter side down is 60%.

Question: If three people drop their slice of toast, what is the probability that one falls butter side down and two fall butter side up?

HINT: Draw trees… Work on this for a few minutes

From proportions to the binomial

First, draw a tree

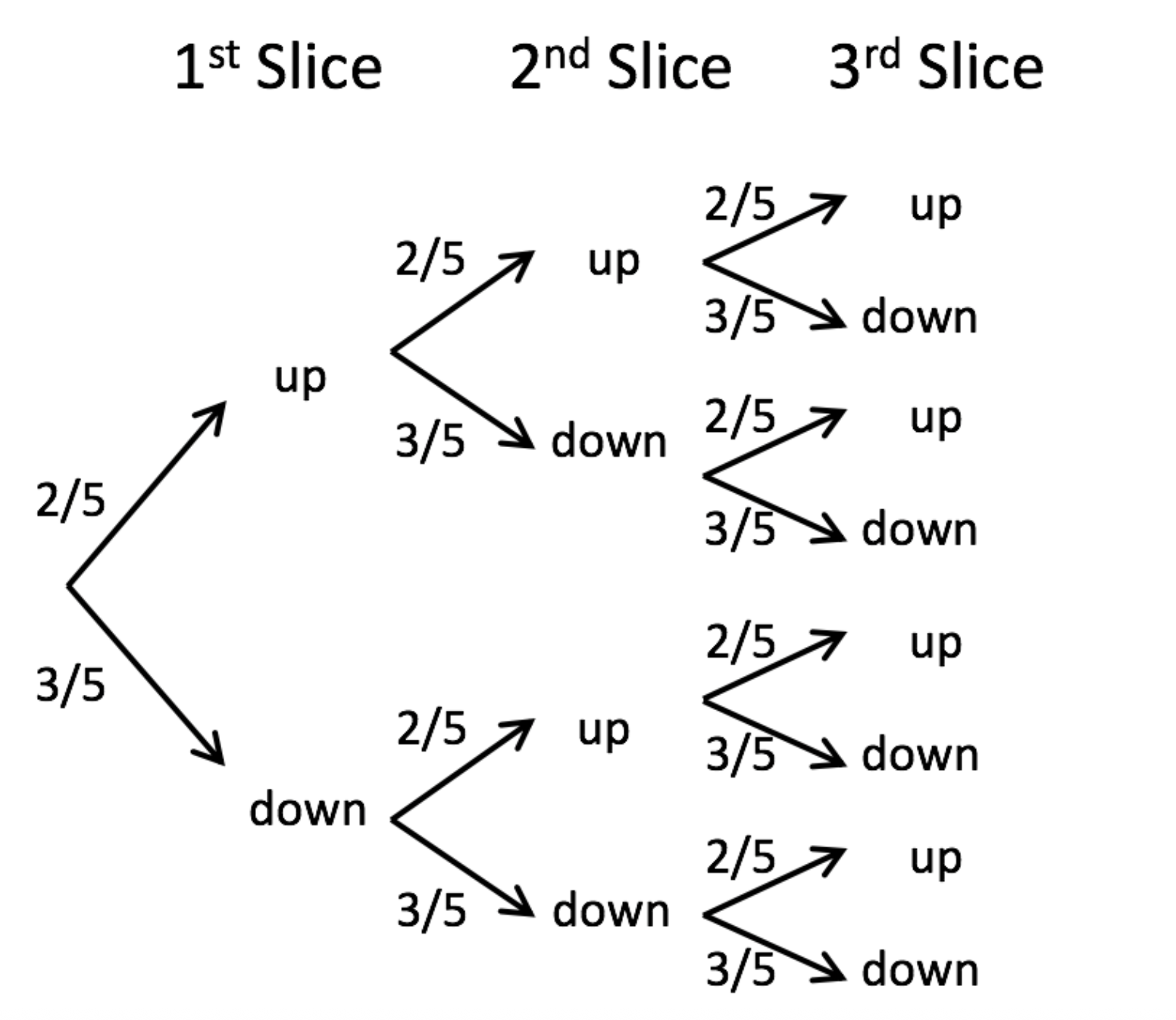
From proportions to the binomial

Then, work out probabilities

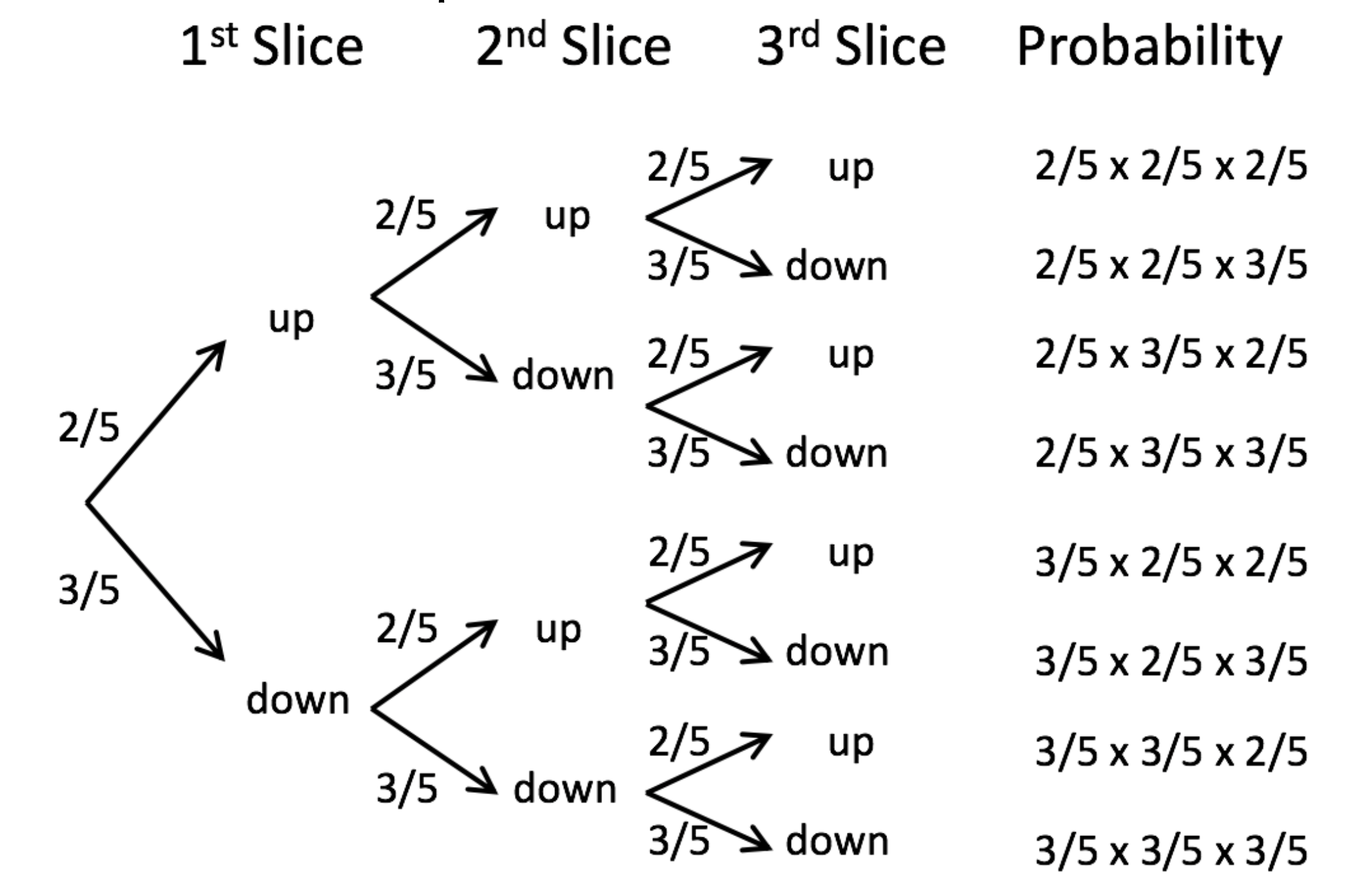
From proportions to the binomial

Finally, count the ways to get the desired outcome

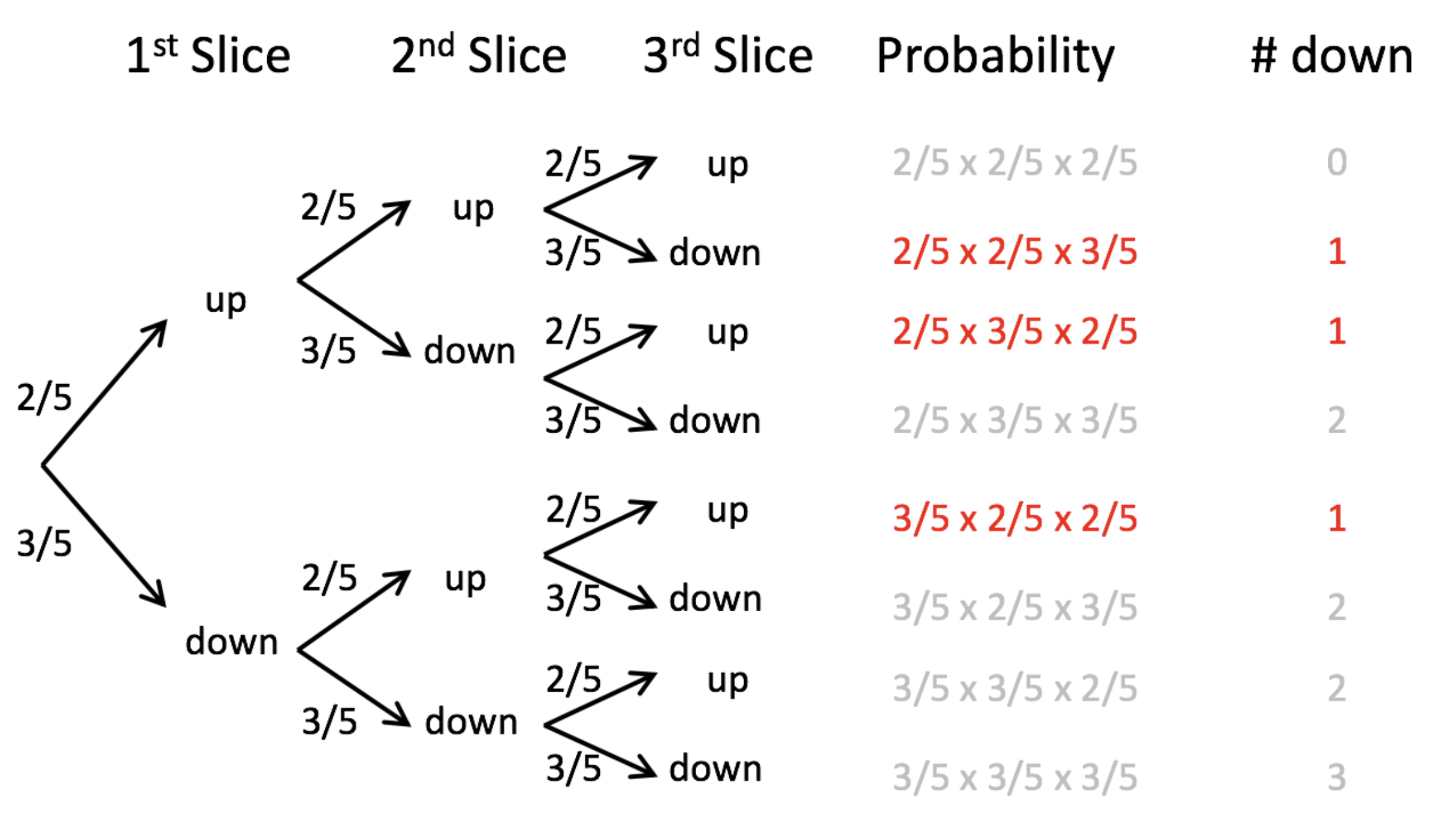
From proportions to the binomial

Add up probabilities

\(3 \times (2/5\times 2/5\times 3/5)=0.288\)

THIS IS OLD NEWS FOR YOU, SO WHAT ELSE IS NEW?

THERE’S AN EASIER WAY: THE BINOMIAL DISTRIBUTION