6.2. Analysing proportions

The binomial test

Bárbara D. Bitarello

2025-11-17

Key learning goals

• Explain probabilities and proportions. Which is the parameter? Which is the estimate?
• Explain the binomial. When would you use it?
• Understand the binomial distribution and connect it to simple probability rules.
• Quantify the expected mean and variability of a binomial distribution.
• Be able to appropriately conduct and interpret a binomial test.

Proportions

• A proportion is the fraction of individuals having a particular attribute. i.e. # successes divided by # trials

• A proportion is also the probability that any an individual randomly sampled from that population will have that attribute

Example: Murphy’s Law

Researchers found that 6101 of the 9821 slices of toast thrown in the air landed butter side down. What proportion of the slices landed butter side down? Is the deck stacked against us?

How would you test this?

From proportions to the binomial

Let’s use this estimated proportion as our best estimate for the true probability of landing butter side down. To make the math a little easier, let’s assume that the true probability that toast falls butter side down is 60%.

Question: If three people drop their slice of toast, what is the probability that one falls butter side down and two fall butter side up?

HINT: Draw trees… Work on this for a few minutes

From proportions to the binomial

First, draw a tree

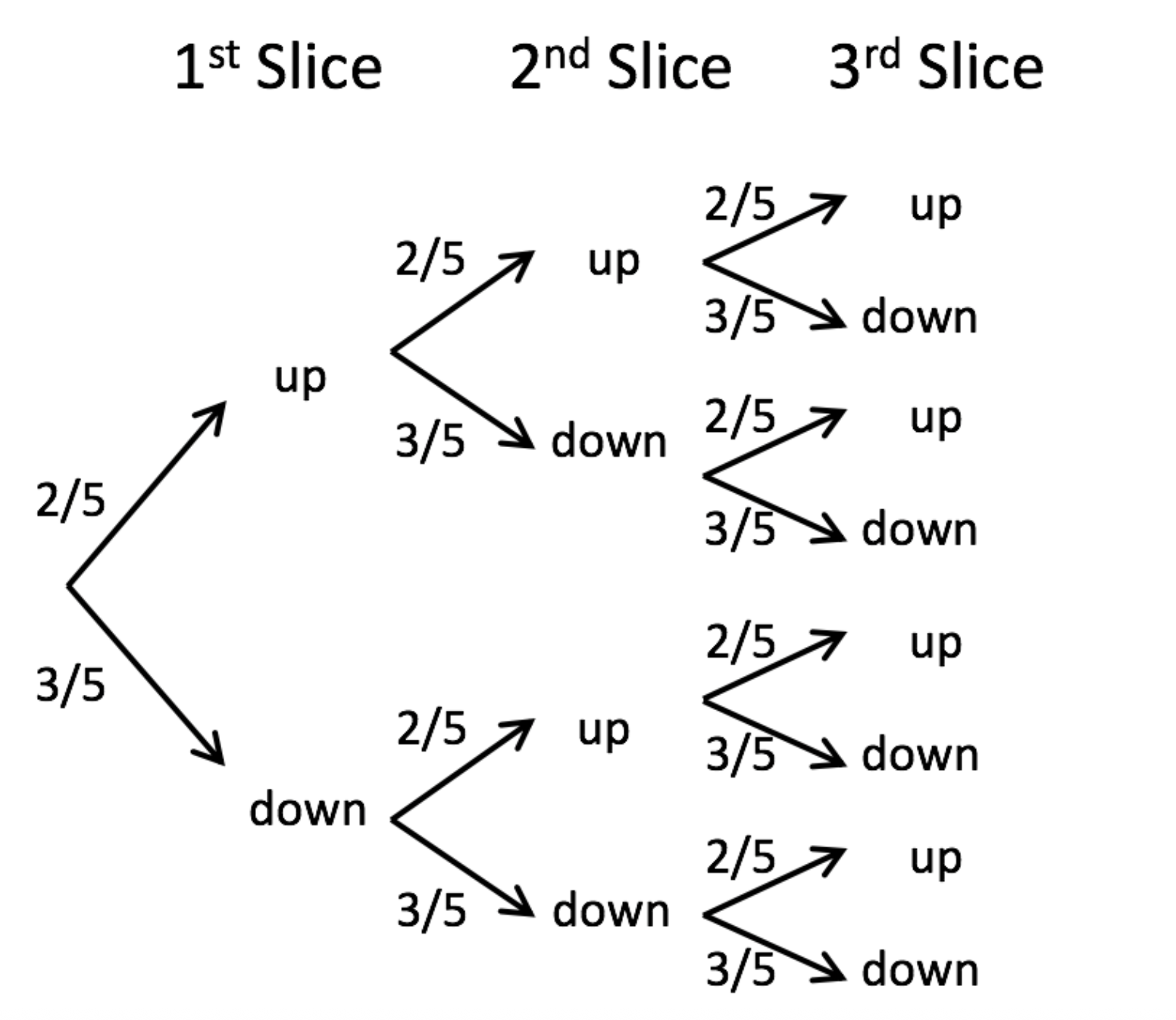
From proportions to the binomial

Then, work out probabilities

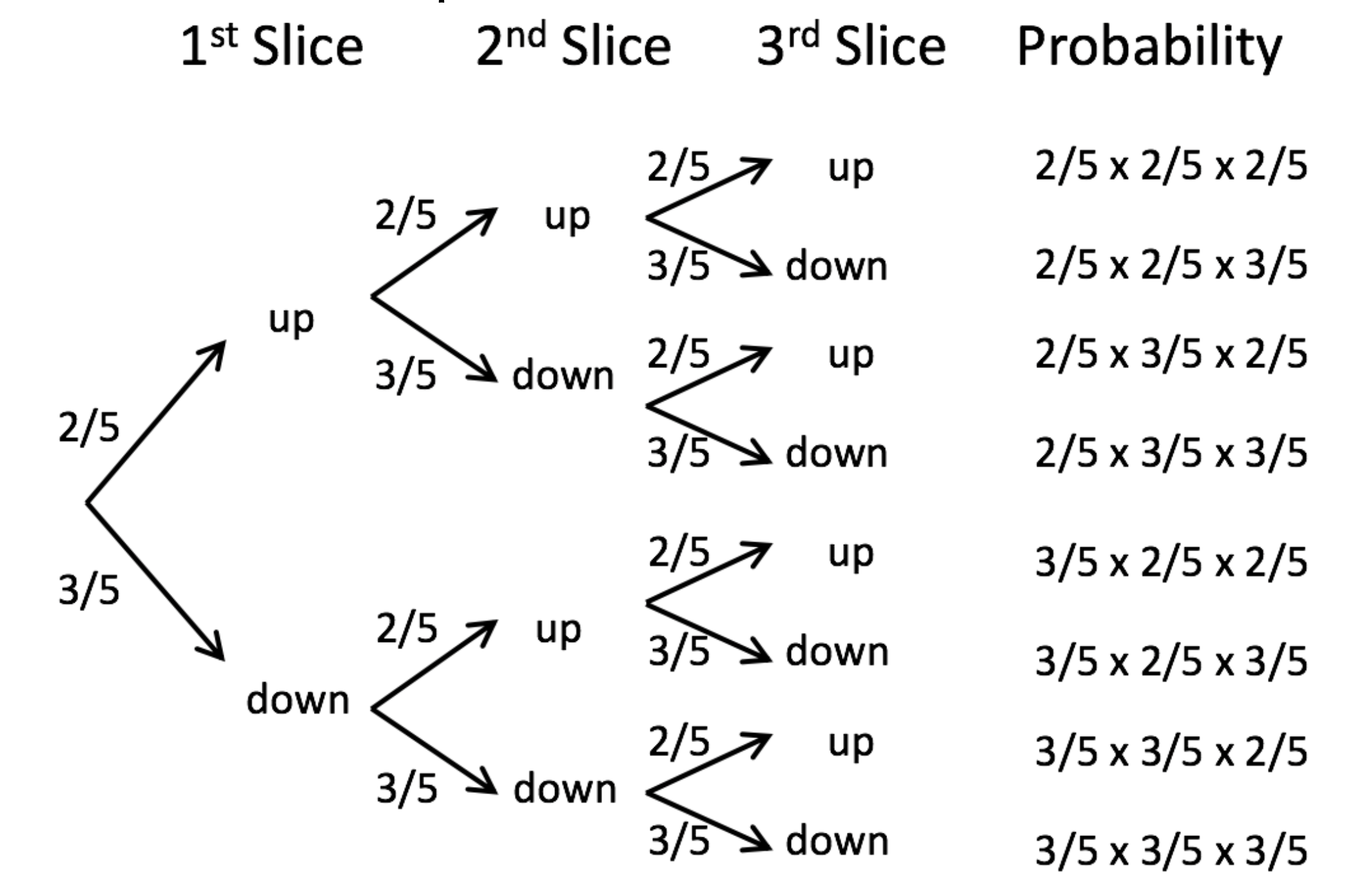
From proportions to the binomial

Finally, count the ways to get the desired outcome

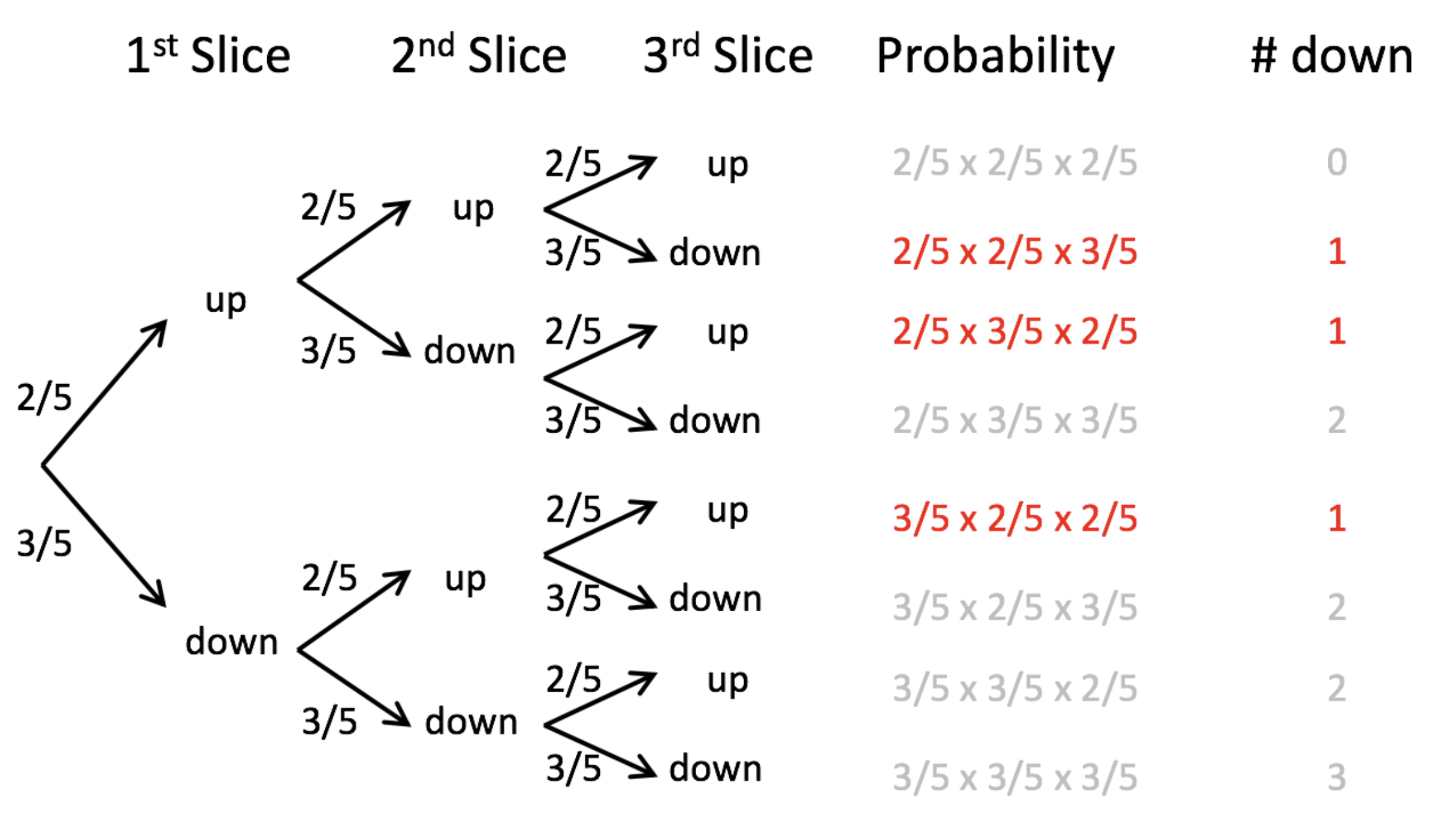
From proportions to the binomial

Add up probabilities

\(3 \times (2/5\times 2/5\times 3/5)=0.288\)

THIS IS OLD NEWS FOR YOU, SO WHAT ELSE IS NEW?

THERE’S AN EASIER WAY: THE BINOMIAL DISTRIBUTION

The Binomial Distribution: Idea

• The probability of a given number (X) of “successes” from a fixed number of n independent trials.

• E.g. If three people drop their slice of toast, what is the probability that one falls butter side down and two fall butter side up?

Probability of Successes

Of \(n\) independent trials, each with probability of success \(p\), the probably of \(X\) successes is given by:

\[P[X]=\binom {n}{X}p^X(1-p)^{n-X}\]

Let’s look at these parts separately

Probability of Successes

\(\binom{n}{X}\): Binomial coefficient: describes the number of ways to get X successes in \(n\) trials.

\(\binom {n}{X}=\frac{n!}{X!(n-X)!}\)

\(n!=n\times (n-1) \times (n-2) ...\times 2 \times 1\)

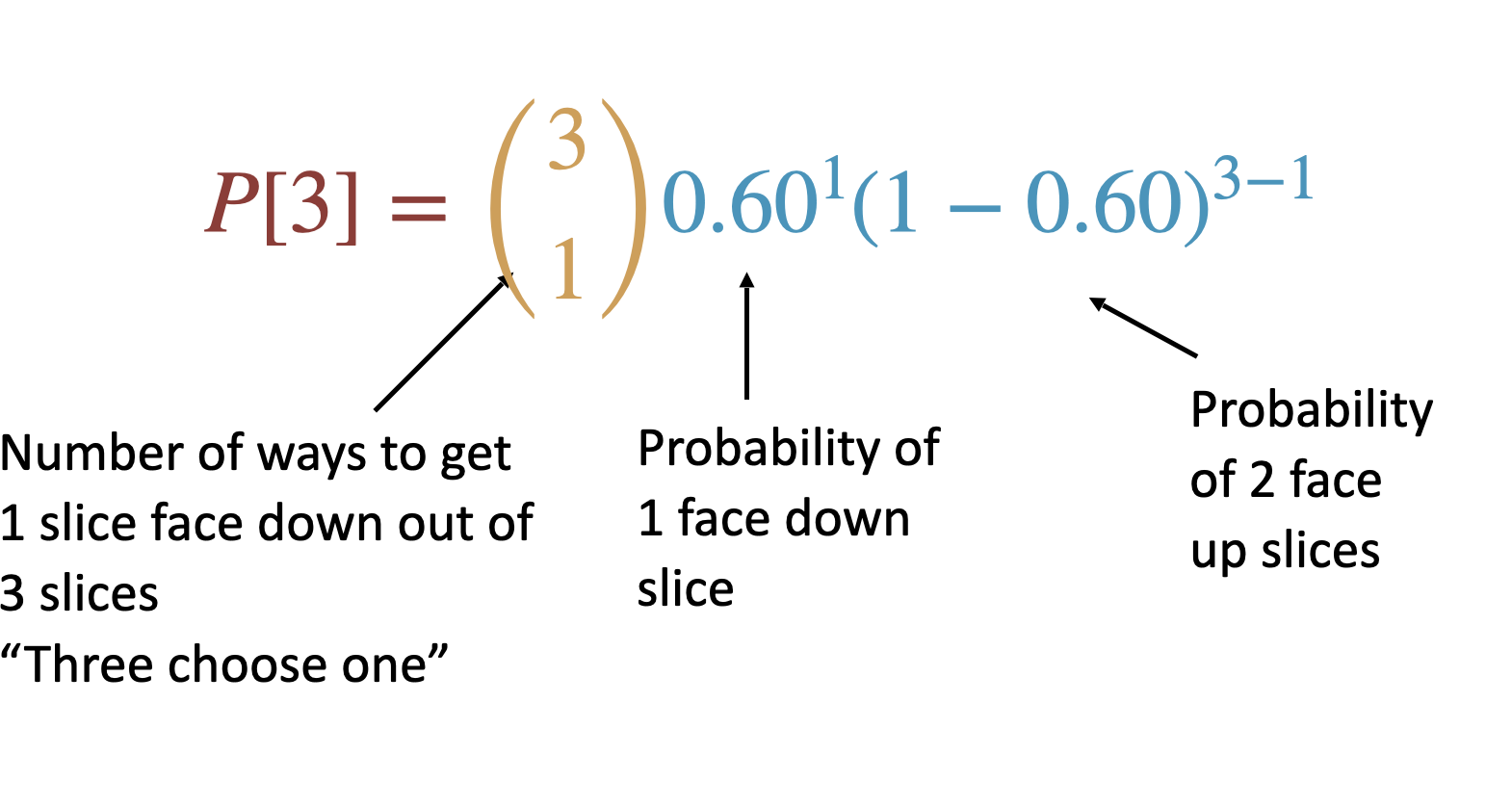
E.g. how many ways are there to toss 3 coins and get 1 tails.

\[\binom {3}{1}=\frac{3!}{1!(2)!}\] \[\binom {3}{1}=3\]

Probability of successes

\(P[X]\): The probability of observing \(X\) successes in \(n\) trials EQUALS

\(\binom{n}{X}\): # ways to get \(X\) successes from \(n\) trials TIMES

\(p^X(1-p)^{n-X}\): The probability of \(X\) successes and by \(n – X\) failures

So back to our toast example

Assume that the true probability that toast falls butter side down is 60%.

Question: If three people drop their slice of toast, what is the probability that one falls butter side down and two fall butter side up?

Step 1: binomial coefficient

\(\binom {n}{X}=\frac{n!}{X!(n-X)!}\)

\(\binom {3}{1}=\frac{3!}{1!(3-1)!}=\frac{3\times 2}{2}=3\)

In R:

# binom coef.  k is a more common notation than X for the binomial coefficient.

# 'n choose k' number of ways to get 1 success out of 3 trials

choose(n = 3, k = 1)
## [1] 3

Toast example (cont.)

Step 2: The probability of \(X\) successes and \(n-X\) failures

\(p^X(1-p)^{n-X}\)

\(0.60\times(1-0.60)^{3-1}=0.60\times 0.40^2=0.096\)

Putting it all together:

\(P[\text{1 successes}]=3\times0.096=0.288\)

Toast example (in R)

“Manually”:

choose(n = 3, k = 1) * 0.6 * (0.4)^(2)
## [1] 0.288

Dedicated function:

dbinom(x = 1, size = 3, prob = 0.6)
## [1] 0.288

More problems!

Problem 2: A population of paradise flycatchers

The population has 80% brown males and 20% white.You capture 5 male flycatchers at random. What is the chance that 3 of those are brown and 2 are white?

\(P[X]=\binom {n}{X}p^X(1-p)^{n-X}\)

\(\binom {n}{X}=\frac{n!}{X!(n-X)!}\)

[work on this for a few minutes]

Problem 2: Solution

\(P[X]=\binom {n}{X}p^X(1-p)^{n-X}\)$

\(\binom {n}{X}=\frac{n!}{X!(n-X)!}\)

\(\binom {n}{X}=\frac{5!}{3!(2)!}\)

\(P[2]=\frac{120}{12}\times 0.8^X(1-0.8)^{5-3}\)

\(=19 \times (0.8)^3\times (0.2)^2\)

\(=0.205\)

Problem 2: Solution in R

In R

# Manually
binom_coef <- (5 * 4 * 3 * 2)/((3 * 2) * 2)
binom_coef * (0.8^3) * ((1 - 0.8)^2)
## [1] 0.2048
# or
binom_coef2 <- choose(n = 5, k = 3)
binom_coef2 * (0.8^3) * ((1 - 0.8)^2)
## [1] 0.2048

Or:

dbinom(x = 3, size = 5, prob = 0.8)
## [1] 0.2048

Problem 2: Solution in R

# notice that success can be either outcome: five birds, 3 brown, 2 white.
# p(brown)=3/5, p(white)=2/5 brown as success
dbinom(x = 3, size = 5, prob = 0.8)
## [1] 0.2048
# white as success
dbinom(x = 2, size = 5, prob = 0.2)
## [1] 0.2048

The binomial test

Testing \(H_0\) that \(\hat p\) comes

from a population with proportion \(p_0\)

Example: the toast is back!

Researchers found that 6101 of the 9821 slices of toast thrown in the air landed butter side down.

What is the probability that we would see a result this or more extreme if toast has a fifty-fifty chance of landing butter side down?

State the hypotheses

Let’s define butter side down as a “success”

Null hypothesis (\(H_{0}\)):

The sample proportion comes from a population with a probability of success equal to \(p_0=0.5\).

Alternate hypothesis (\(H_{A}\)):

The sample proportion comes from a population with a probability of success \(\neq p_0\).

Calculate test statistic:

\(p_0 = .5\), \(n = 9821\), \(X = 6101\)

\(\hat p=\frac{X}{n}=\frac{6101}{9821}=0.62\)

Generate the null & Find P-value

Actually calculating P-value would look like this

\(9821-6101=3719\)

Two-tailed P-value:

\(p = \sum_{X = 6101}^{X = 9821} {9821 \choose X} .5^X (.5)^{9821-X}\)

\(+\)

\(\sum_{X = 0}^{X = 3719} {9821 \choose X} .5^X (.5)^{9821-X}\)

We conducted a Binomial Test!

We reject \(H_0\) & conclude that toast is more likely to land butter side down than not

👏 Congrats 👏 You already conducted a hypothesis test!

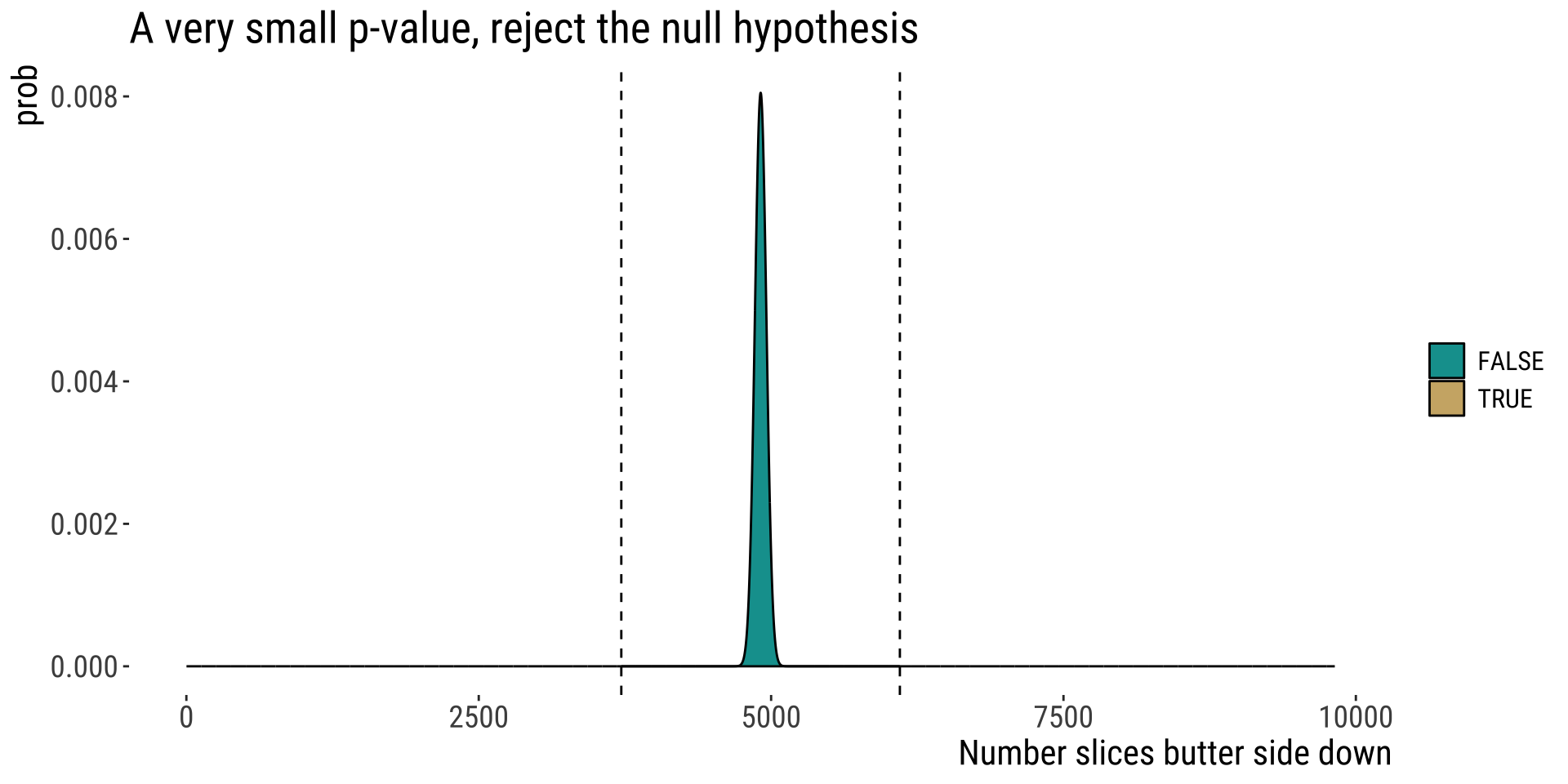
R can make this even easier

butter.down <- 6101
slices <- 9821
prop.down <- butter.down/slices
#
binom.test(x = butter.down, n = slices, p = 0.5, alternative = "two.sided")
## 
##  Exact binomial test
## 
## data:  butter.down and slices
## number of successes = 6101, number of trials = 9821, p-value < 2.2e-16
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.6115404 0.6308273
## sample estimates:
## probability of success 
##              0.6212198
# doing it 'manually'
sum(dbinom(6101:9821, size = 9821, prob = 0.5)) + sum(dbinom(1:((9821 - 6101) + 1),
    size = 9821, prob = 0.5))
## [1] 1.390148e-128

Properties of the binomial distribution

Expected # successes of n trials

Expected successes in \(n\) trials

\[\Huge{\mu = n \times p}\]

\(\mu\): That’s right. Mean number of successes, aka, expected number of successes.

Probability Trivia: A binomial with n = 1 is called a Bernoulli process. This will not be a factoid you need to know in this class, but you might hear it some time.

Binomial: Variability and Uncertainty

For counts:

\[\text{population variance: } \sigma^2 = n \times p \times(1-p)\]

\[\text{sample variance: }s^2 = n\times \hat p \times(1-\hat p)\]

Note: Some textbooks use n-1 rather than n for the denominator of the standard error. Dividing by n-1 decreases bias, but yields estimates results that are further from the truth, on average.

Properties of proportions: expectations

If there are \(X\) successes in \(n\) trials in a random sample, then the

estimated proportion of successes is:

\[\hat p = \frac{X}{n}\]

\(\hat p\): The hat signals that this is an estimate

\(p\): The expected proportion of successes is the probability of success p