6.3. Analysing proportions

The binomial test

Bárbara D. Bitarello

2025-11-18

Properties of the binomial distribution

Expected # successes of n trials

Expected successes in \(n\) trials

\[\Huge{\mu = n \times p}\]

\(\mu\): That’s right. Mean number of successes, aka, expected number of successes.

Probability Trivia: A binomial with n = 1 is called a Bernoulli process. This will not be a factoid you need to know in this class, but you might hear it some time.

Binomial: Variability and Uncertainty

For counts:

\[\text{population variance: } \sigma^2 = n \times p \times(1-p)\]

\[\text{sample variance: }s^2 = n\times \hat p \times(1-\hat p)\]

Note: Some textbooks use n-1 rather than n for the denominator of the standard error. Dividing by n-1 decreases bias, but yields estimates results that are further from the truth, on average.

Properties of proportions: expectations

If there are \(X\) successes in \(n\) trials in a random sample, then the

estimated proportion of successes is:

\[\hat p = \frac{X}{n}\]

\(\hat p\): The hat signals that this is an estimate

\(p\): The expected proportion of successes is the probability of success p

Sample size and standard error

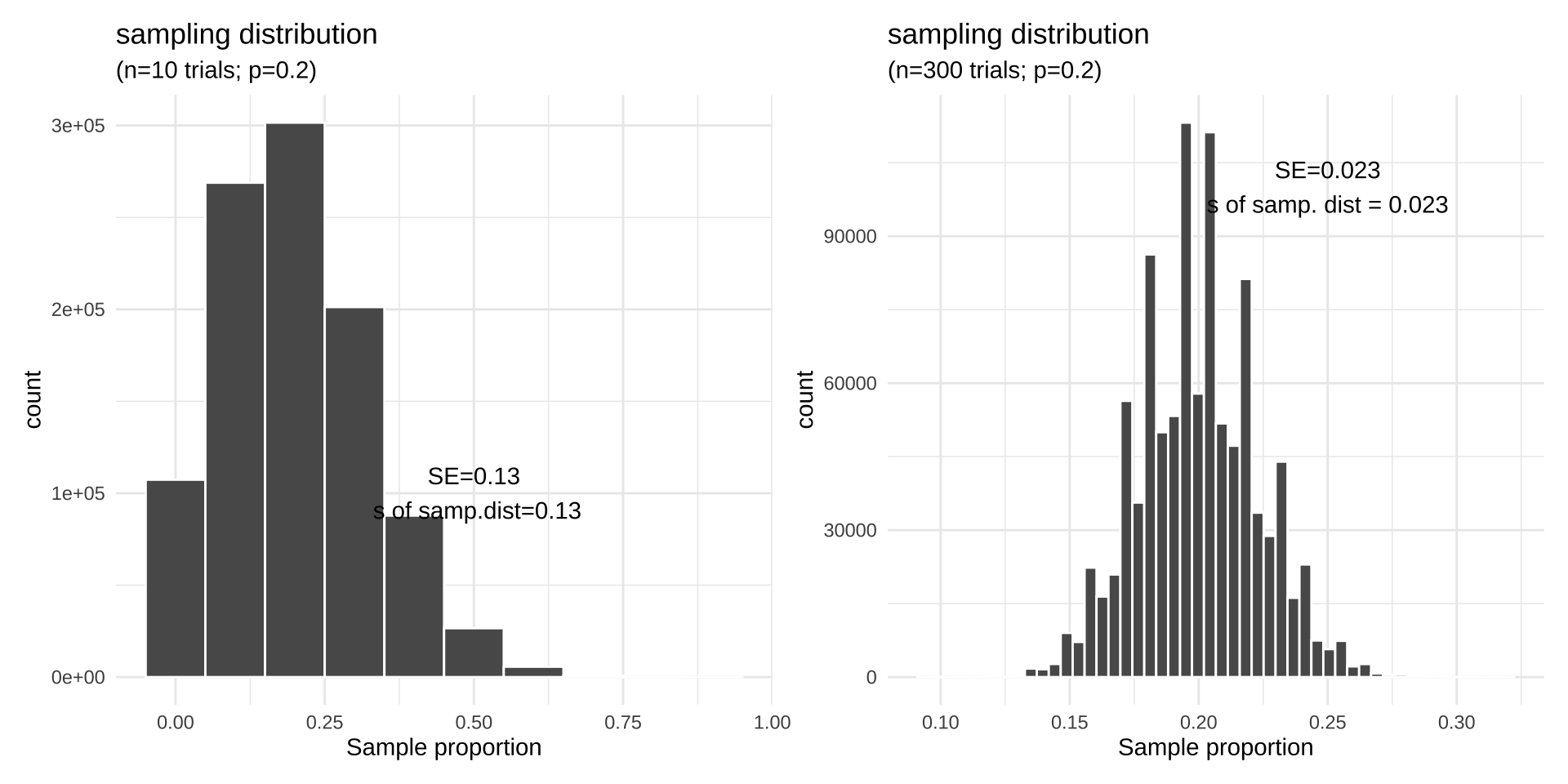
Properties of Proportions: Variability

Variance	\(\sigma^2=p(1-p)\)
Standard deviation	\(\sigma=\sqrt(p(1-p))\)
Sample variance	\(s^2=\hat p(1-\hat p)\)
Sample standard deviation	\(s=\sqrt{\hat p(1-\hat p)}\)

Standard error of a proportion

Recall: the standard error of an estimate is always the standard deviation of its sampling distribution. If we know the real \(p\) we can calculate it as:

\[\sigma_{\hat p}=\sqrt{\frac{p(1-p)}{n}}\]

Because \(p\) is usually unknown, in practice we have:

\[s_{\hat p}=\sqrt{\frac{\hat p(1-\hat p)}{n}}\]

Note: Some textbooks use \(n-1\) rather than n for the denominator of the standard error. Dividing by \(n-1\) decreases bias, but yields estimates results that are further from the truth, on average.

95% CIs for a proportion (1/)

• For many parameter values, the binomial distribution is not symmetric about its mean. This is one reason why the 2 SE rule of thumb does not work for this.
• The 95% confidence interval of a proportion will enclose the true value of the proportion 95% of the time that it is calculated from new data.
• There are many ways to approximate the 95% CI of a proportion, and no consensus[1].

[1]: In R “Confidence intervals are obtained by a procedure first given in Clopper and Pearson (1934). This guarantees that the confidence level is at least conf.level, but in general does not give the shortest-length confidence intervals.” (from help(binom.test) in R)

95% CIs for a proportion (2/)

• The book suggests the Agresti-Coull CIs:

\[\bigg(p' - 1.96 \sqrt{\frac{p'(1-p')}{n+4}}\bigg) \leq p \leq \bigg(p' + 1.96 \sqrt{\frac{p'(1-p')}{n+4}}\bigg)\]

\(p' = (X+2) / (n+4)\)… where \(X =\) observed # of successes

[1]: In R “Confidence intervals are obtained by a procedure first given in Clopper and Pearson (1934). This guarantees that the confidence level is at least conf.level, but in general does not give the shortest-length confidence intervals.” (from help(binom.test) in R)

Approximations for the Binomial Test

Why?

• Adding up all the probabilities to obtain the exact p- value is pretty time-consuming

• Because of that, two approximations for the p-value of a binomial test exist: the chi-square goodness-of-fit test (next topic) and the normal approximation to the binomial test

• They can be useful and are very common.

• In R you can implement the exact binomial test easily, though, as we saw

If asked to conduct a binomial test by hand, you can use the chi-squared approximation to get a p-value

Key Points

• A proportion is an estimate of a probability.

• The binomial distribution provides a clear example of building up from simple probability logic to mathematical models of probability.

• The binomial test tests the null hypothesis that an estimated proportion comes from a population with a specified probability.

• We can quantify the uncertainty in our estimate of the probability.

Interactive App: https://shiny.rit.albany.edu/stat/binomial/