4.1.Estimation with Uncertainty

Bárbara D. Bitarello

2025-10-22

Key Learning Objectives

• Understand that because estimates take values by chance, they will differ from true population parameters.
• Connect the spread of the sampling distribution to uncertainty in estimates.
• Recognize the standard error as the standard deviation of the sampling distribution.
• Understand the confidence interval as a plausible range of a parameter, given an estimate and uncertainty in it.

Samples Take Their Value by Chance

• Sets of samples from the same distribution can be different.

• Therefore, estimates obtained from samples from the same population can differ by chance.

Note: This unit focuses on sampling error and assumes that samples are not biased - i.e, they are random.

Samples: what’s the point?

• We sample because we cannot measure the entire population.

• When we take samples, we cannot see the sampling distribution.

• Still, considering the process of sampling allows us to quantify the uncertainty in estimates.

Estimation: from samples to parameters (hopefully)

Two Ways to Conceptualize Sampling

Okay, so how do we do this?

Here are the two right* ways to think about the process of taking a sample from a population.

1. If you had a full population and made an estimate from a sample of size \(n\).

2. Think about the PROCESS that generates your population data: what would a sample generated by this process look like? (e.g. flipping a coin).

• But sometimes one is more convenient than the other.

Some definitions

Estimation: a process of inferring a population parameter from sample data. This estimated value is almost never exactly identical to the true parameter value.

Sampling error affects precision of estimates. It is basically inevitable because it is inherent to random sampling.

Note: This unit focuses on sampling error and assumes that samples are not biased - i.e, they are random.

Generating samples from a population

In two easy steps:

1. Take a sample of size n.

2. Calculate the parameter estimates.

This is how we do science.

Example

A Population of Diamonds

A population of 180 diamonds of different sizes and colors.

	small	medium	large
blue	18	24	9
gold	42	24	18
red	21	24	0

A sample of 20 diamonds

star.sample.size <- 20
stars.sample <- sample_n(stars, size = star.sample.size, replace = FALSE)
ggplot(stars.sample, aes(x = x, y = y, color = color, size = size)) +
  geom_point(shape = 18, show.legend = FALSE) + 
  scale_color_manual(values = asteroidcity1()) +
  bb_theme() + 
  ylab("") + 
  xlab("") +
   theme(axis.text.x = element_blank(), axis.text.y = element_blank())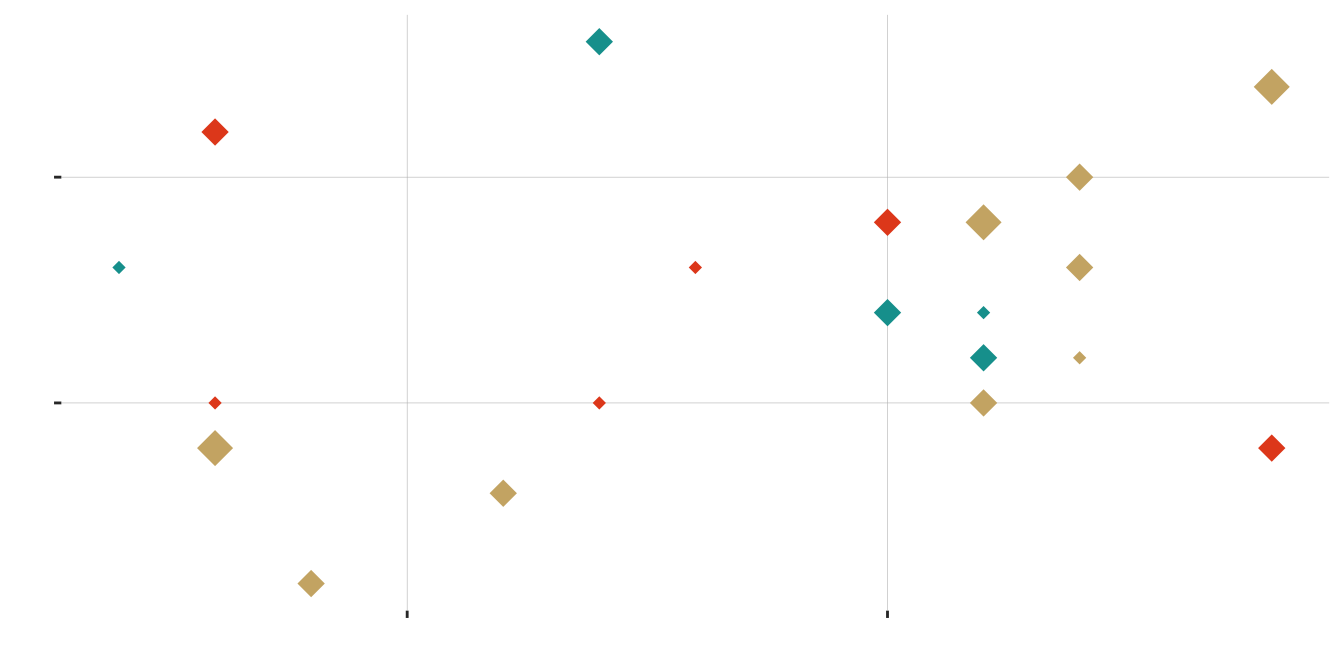

	small	medium	large
blue	2	3	0
gold	1	5	3
red	3	3	0

Another sample of 20 diamonds

star.sample.size <- 20
stars.sample <- sample_n(stars, size = star.sample.size, replace = FALSE)
ggplot(stars.sample, aes(x = x, y = y, color = color, size = size)) +
  geom_point(shape = 18, show.legend = FALSE) + 
  scale_color_manual(values = asteroidcity1()) +
  bb_theme() + 
  ylab("") + ylab("") +   
  theme(axis.text.x = element_blank(), axis.text.y = element_blank())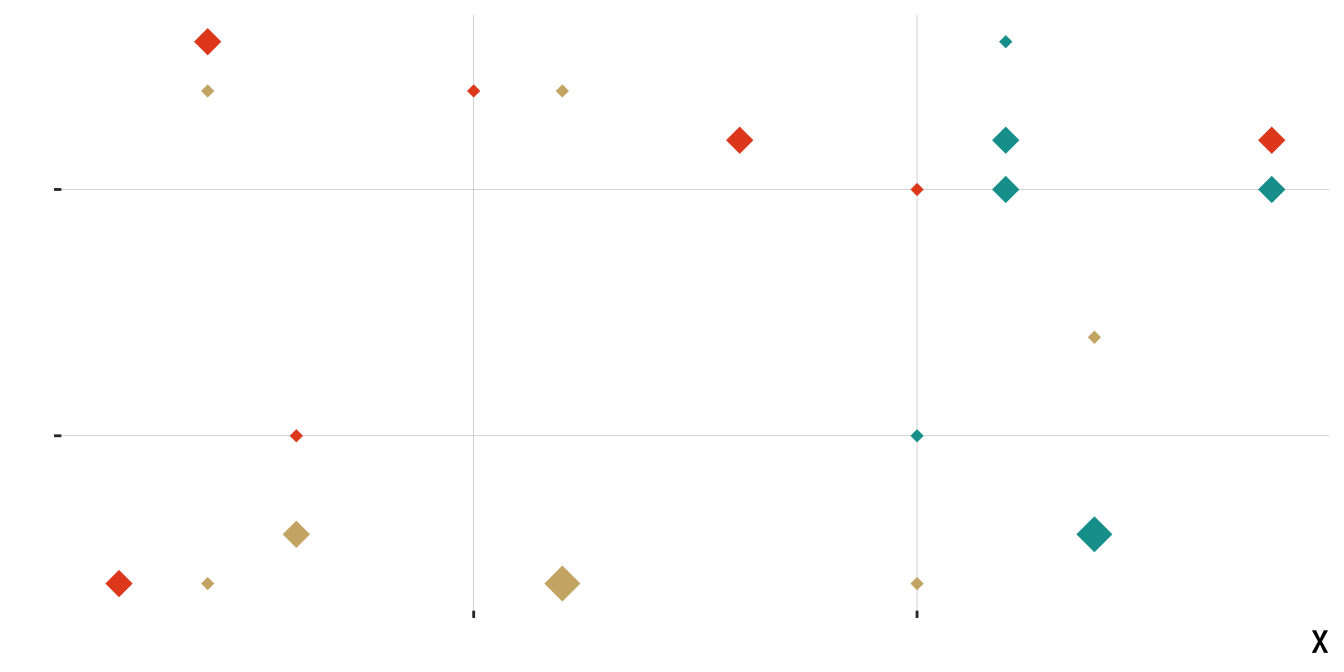

	small	medium	large
blue	2	3	1
gold	5	1	1
red	3	4	0

Aaaand … another

star.sample.size <- 20
stars.sample <- sample_n(stars, size = star.sample.size, replace = FALSE)
ggplot(stars.sample, aes(x = x, y = y, color = color, size = size)) +
  geom_point(shape = 18, show.legend = FALSE) + 
  scale_color_manual(values = asteroidcity1()) +
  bb_theme() + 
  ylab("") + 
  xlab("") +
   theme(axis.text.x = element_blank(), axis.text.y = element_blank())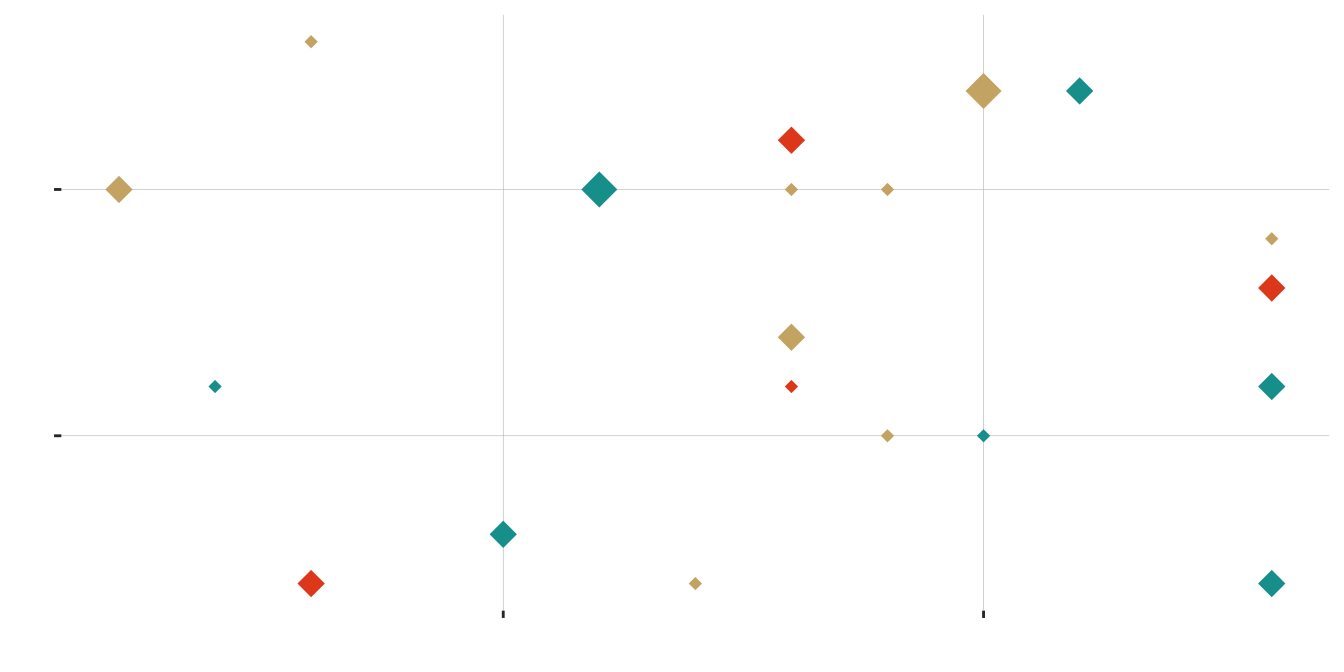

	small	medium	large
blue	2	4	1
gold	6	2	1
red	1	3	0

One Last Sample of 20 Diamonds

star.sample.size <- 20
stars.sample <- sample_n(stars, size = star.sample.size, replace = FALSE)
ggplot(stars.sample, aes(x = x, y = y, color = color, size = size)) + geom_point(shape = 18,
    show.legend = FALSE) + scale_color_manual(values = asteroidcity1()) + bb_theme() +
    ylab("") + xlab("") + theme(axis.text.x = element_blank(), axis.text.y = element_blank())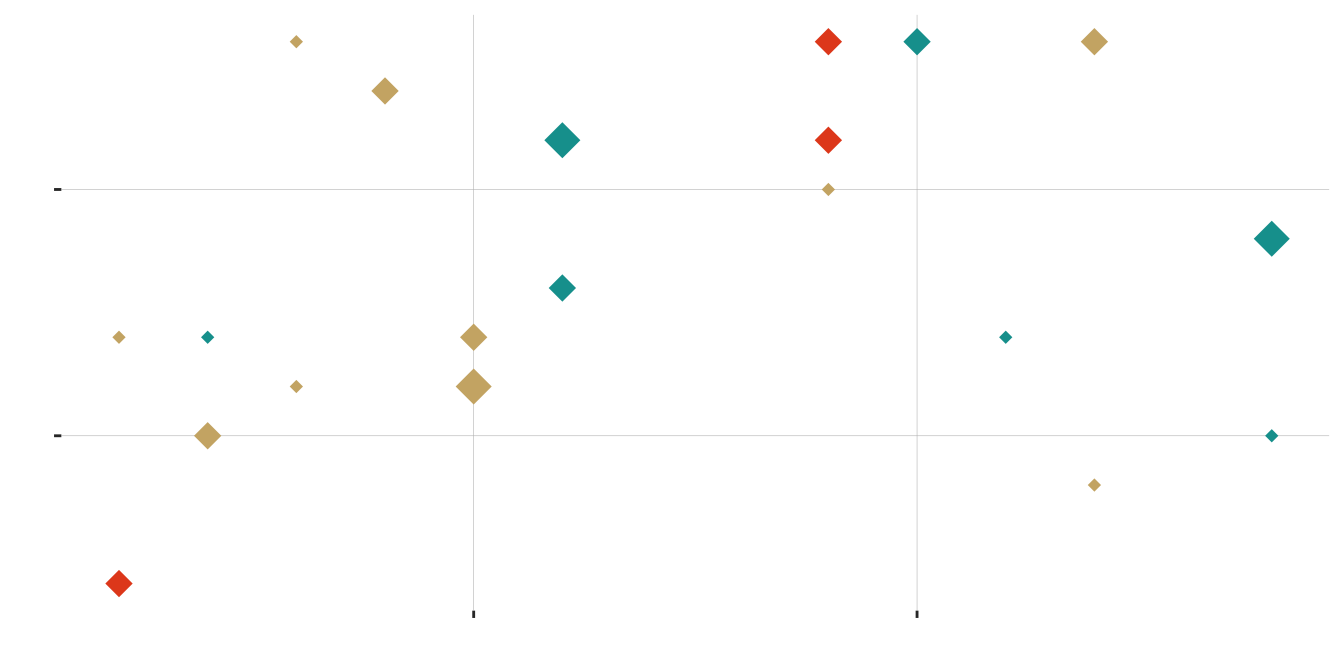

	small	medium	large
blue	3	2	2
gold	5	4	1
red	0	3	0

Sampling Diamonds: Lessons Learned

1. “Sampling is random”

   Estimates from sampling efforts varied and did not perfectly capture the true population values. I.e, there is sampling error involved.

2. Random DOES NOT mean that all outcomes are equally probable. E.g.:

• There are no LARGE RED diamonds in the population so we never sampled a LARGE RED diamond.

• The most common diamond color in the population is gold. Gold is often the most common color in a sample.

There are some other great interactive simulators out there to help you grasp the sampling distribution. I share one later.

The sampling distribution!

The sampling distribution

• The sampling distribution is the distribution of the parameter estimate of interest from these samples

• It is basically a histogram of all the values that a sample statistic can take on

• They are super important: when you take a sample from a population, you base your conclusions on that sample, but we know samples vary randomly (even in the absence of bias)

• To be able to interpret your sample results (say, mean bill length in a sample of 20 penguins from a given population) you need they stand amongst the “crowd”

• The “crowd” of all possible sample statistics you can possibly get is the sampling distribution

Generating a sampling distribution

In three easy steps:

1. Take a sample of size \(n\).

2. Calculate the parameter estimates.

3. Rinse and repeat many times.

Assumption: you can sample repeatedly from the population of interest and your sampling does not in iteself change the population of interest. When this is not possible to do, you can bootstrap! (which we did in Lab 6, more on this later). In the meantime, check this out.

Example: The Sampling Distribution of Diamonds

replicate	color	small	medium	large
1	blue	0.25	0.10	0.05
1	gold	0.25	0.10	0.05
1	red	0.00	0.20	0.00
2	blue	0.05	0.05	0.00
2	gold	0.30	0.30	0.05
2	red	0.05	0.20	0.00
999	blue	0.15	0.15	0.05
999	gold	0.25	0.10	0.15
999	red	0.00	0.15	0.00
1000	blue	0.10	0.15	0.00
1000	gold	0.25	0.05	0.10
1000	red	0.15	0.20	0.00

Sampling distribution of diamond size

replicate	small blue	small gold	small red	medium blue	medium gold	medium red	large gold	large blue
1	4	3	4	2	2	4	1	0
2	2	7	3	5	0	1	2	0
999	1	7	4	1	3	2	1	1
1000	2	6	3	4	2	1	1	1

Sampling distribution of diamond size

ggplot(sampling.dist.large, aes(x = prop)) + 
  geom_histogram(binwidth = 1/ star.sample.size, color = "lightgray", fill = "#006475")+
  geom_vline(xintercept = true.prop.large, lty = 2, color = "white") +
  ggtitle(sprintf("Sampling distribution: Proportion large diamonds (n = %s)", star.sample.size),
          subtitle = "Dotted white line is the population parameter") +
  xlab("proportion")+
  ylab("# of replicates\n(of 1000 simulations)")+
  bb_theme()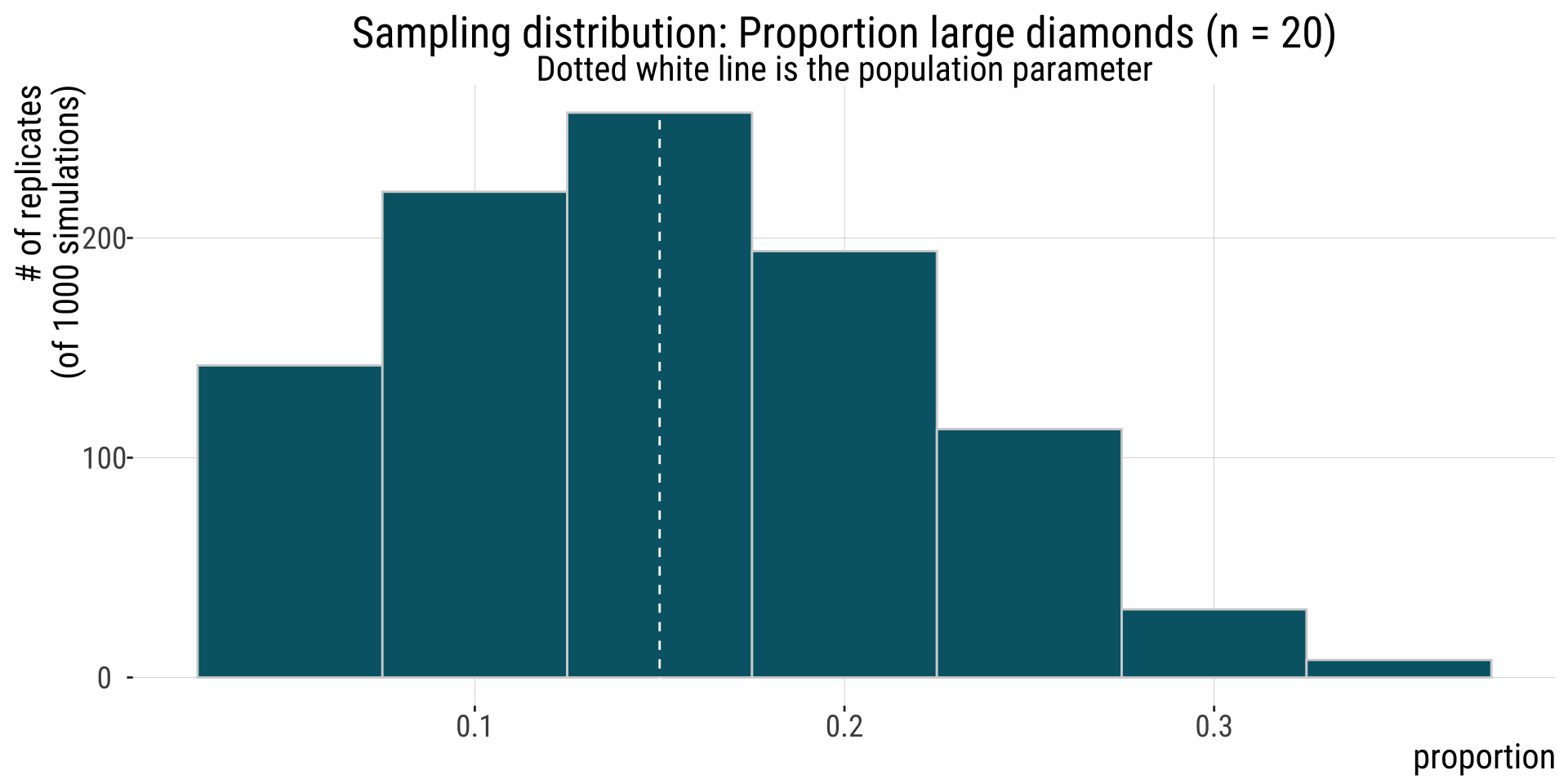

The joint sampling distribution

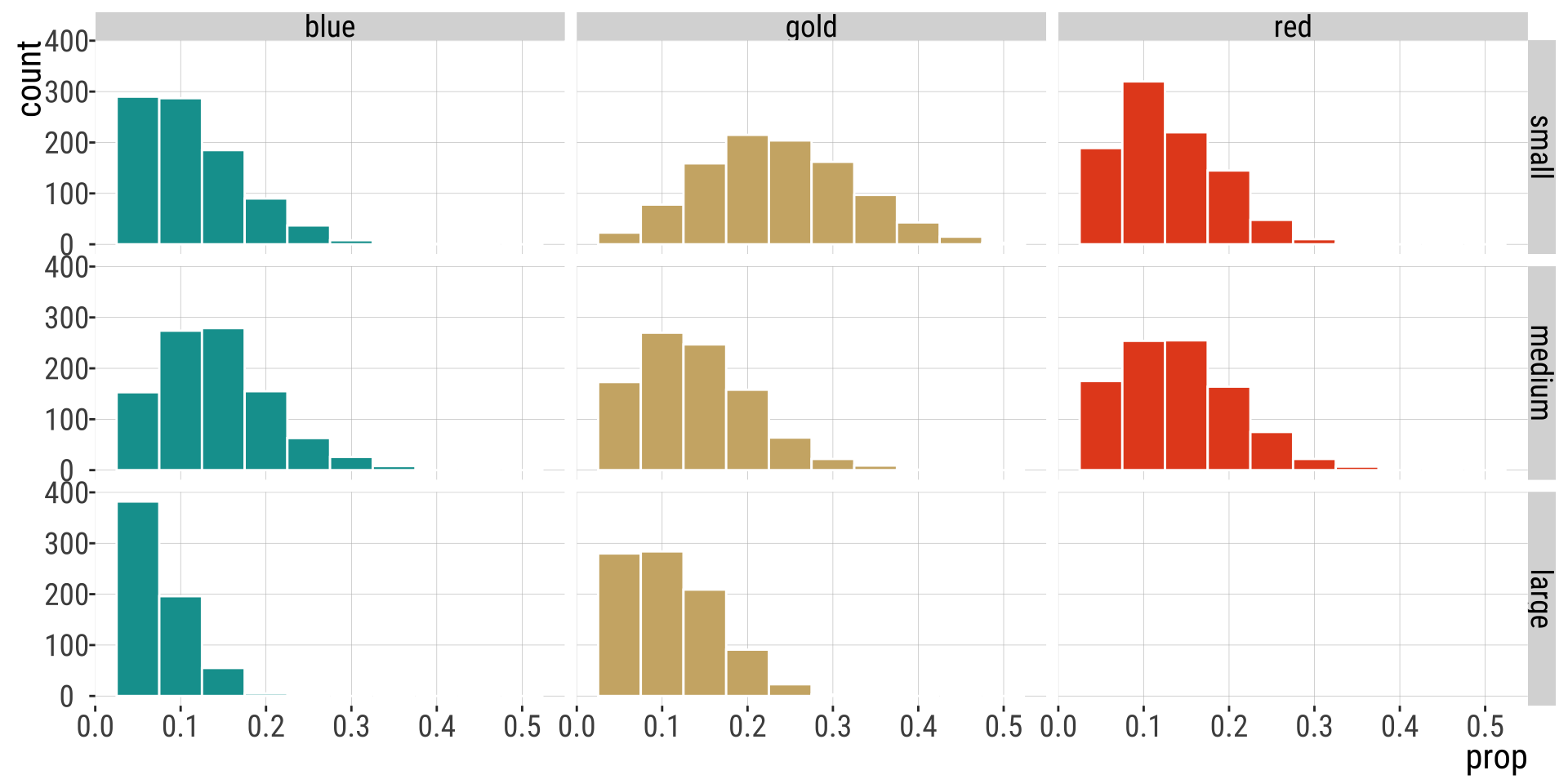
How does variability in an estimate change with sample size?

Variability in Estimates Decreases with N

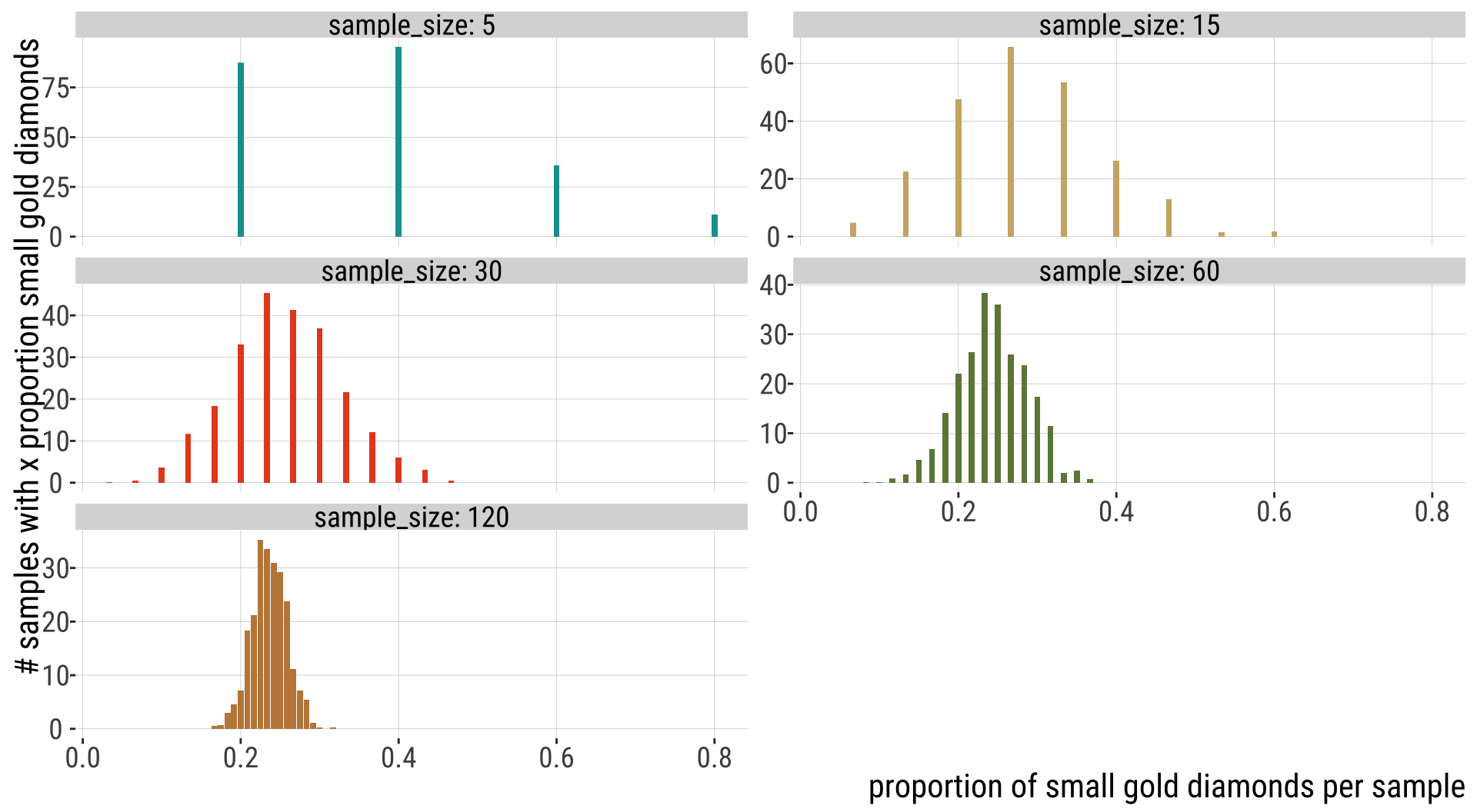
Variability in Estimates Decreases with N

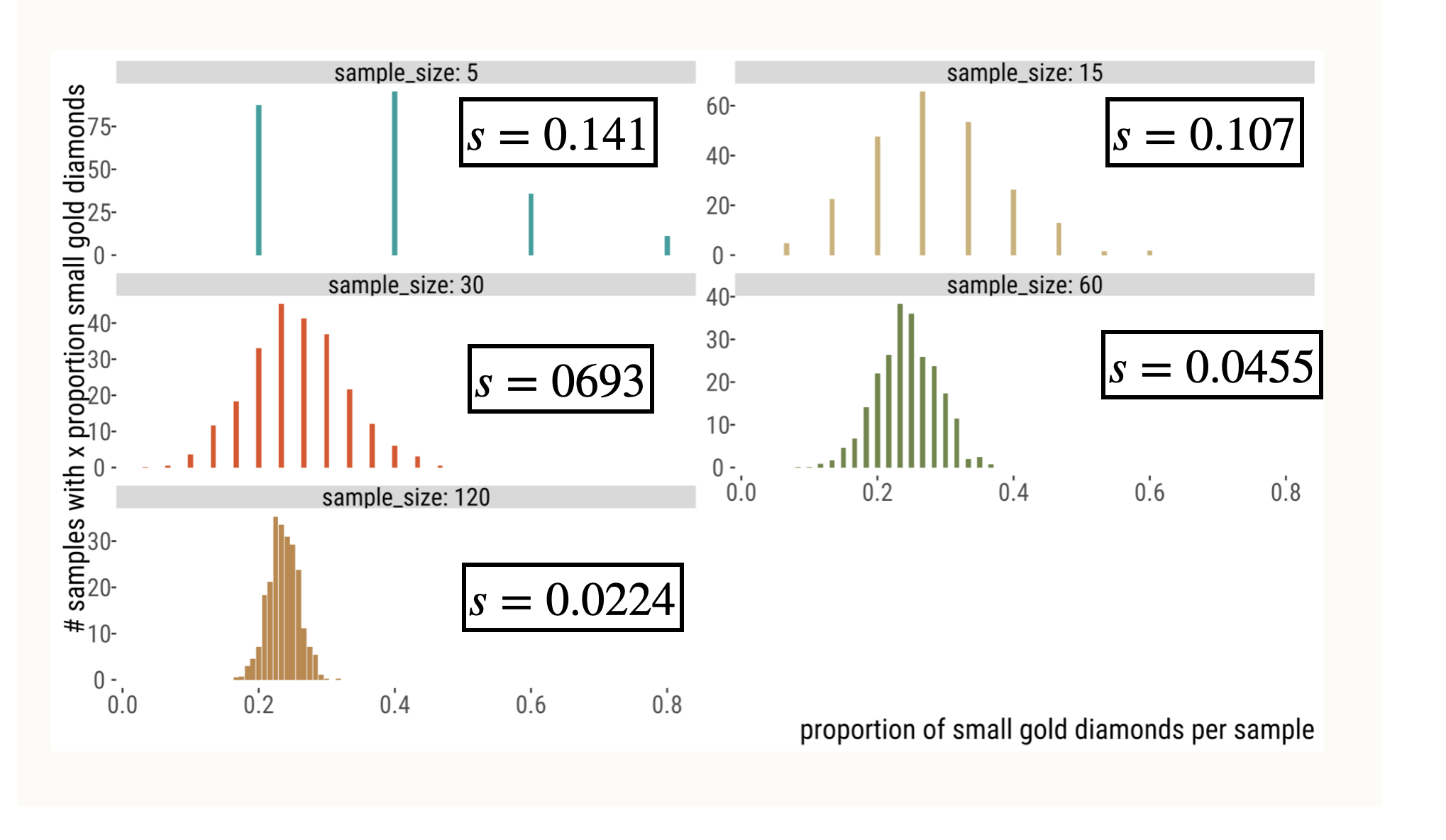
Standard Error

The Standard Error: Definition

• The standard error reflects the difference between an estimate and the target parameter value.

• The standard error predicts the sampling error of the estimate.

The Standard Error of the Mean (SEM)

• Because we rarely know the population standard deviation,\(\sigma\), we cannot find the parameter \(\sigma_{\bar{Y}}=\frac{\sigma_{Y}}{\sqrt{n}}\) , the standard error of the population mean.

• But, we can use the sample standard deviation, \(s\), to estimate \(SEM_{\bar{Y}}=\frac{s}{\sqrt{n}}\), the standard error of the sample mean.

Also:

The standard error of an estimate is the standard deviation of its sampling distribution!

Example: human gene lengths

Human gene lengths

ggplot(human_genes , aes(x=size)) + geom_histogram(aes(y=after_stat(count / sum(count))),bins=60, color="lightgray", fill="#006475") + xlab("Gene Length (basepairs)") + 
  ylab("Relative Frequency")+
  annotate('text', x = 10000, y = 0.04, 
        label = "mu==3511.5",parse = TRUE,size=10) +
  annotate('text', x = 10000, y = 0.03, 
        label = "sigma==2833.2",parse = TRUE,size=10)+
  bb_theme()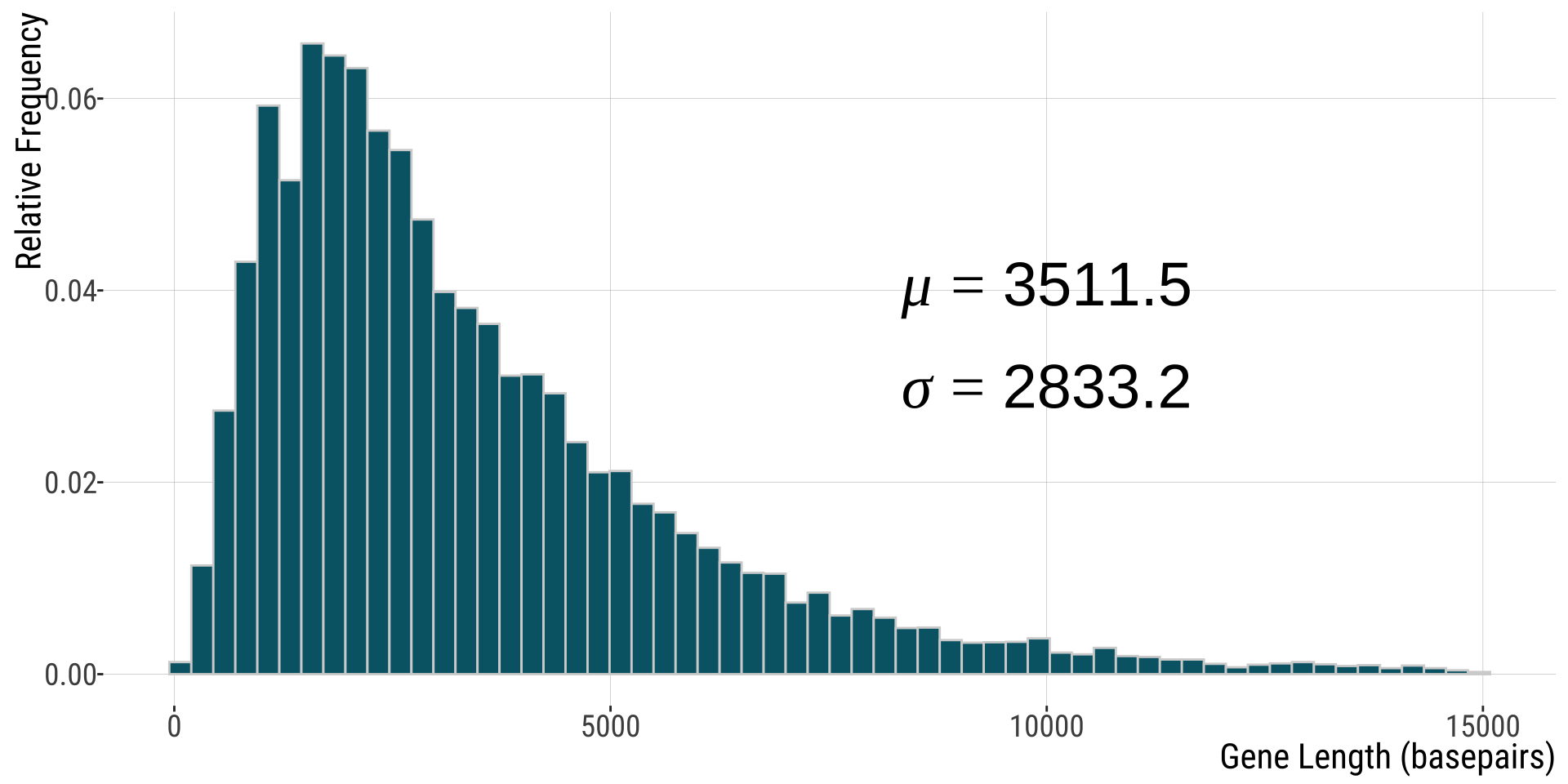

Note: parameters shown are for full dataset (n=20,290) but 26 genes with length > 15,000 were omitted from this plot.

Sampling Distribution: from textbook

Click on the figure to go to the Web App

That’s all for today

From: makeameme.org