Acknowledgments: many code snippets borrowed from Y. Brandvain
2025-10-06
Example: what’s the probability that a fair die will give me 2 if I roll it once?
Figure caption: figure 5.2-1 from the textbook.
Example: Probability of getting a 4 in one roll (trial) of a six-sided die
A random trial is a process or experiment that has two or more possible outcomes whose occurrence cannot be predicted with certainty.
Only one outcome is observed from each repetition of a random trial.
Figure caption: figure 5.2-1 from the textbook.
Example: possible numbers in a die roll
Mutually Exclusive
If \(A\) and \(B\) are mutually exclusive:
even_numbers <- c(2, 4, 6)
odd_numbers <- c(1, 3, 5)
l <- list(even = even_numbers, odd = odd_numbers, all = sort(c(even_numbers, odd_numbers)))
library(ggvenn)
p1 <- ggvenn(l[c(1:2)], fill_color = asteroidcity1(), show_elements = TRUE, text_size = 12) +
ggtitle("Cannot be even AND odd") + theme(plot.title = element_text(family = "Roboto Condensed",
size = 20))
p1
E.g., \(P(\text{even AND odd})=0\) in a die roll
Example: possible numbers in a die roll
Non-mutually exclusive
If \(A\) and \(B\) are not mutually exclusive:
E.g., \(P(\text{even AND prime}) \neq 0\) in a die roll – in fact, what is it?
Probability distributions describe discrete variables.
Probability distributions sum to 1.
\(\sum{p[x]}=1\)
All possible values: \(x=\{1,2,3,4,5,6\}\)
Probabilities of particular outcomes: \(p[1]=1/6\)
\(p[2]=1/6,\text{etc}\)
Sum of probabilities of all possible outcomes:
\(\sum{p[x]}=1\)
The probability of any value from a continuous distribution is infinitesimally small.
Probability densities integrate to 1.
\(\int{p[x]}=1\)
Area under the curve gives you the probability of values in a range \(\left[a,b\right]\) Each value has an an infinitesimal probability value
Figure caption: figure 5.4-4 from the textbook.
plot.one.dice.prob <- data.frame(outcome = c(1:6), probability = 1/6) |>
ggplot(aes(x = outcome, y = probability, fill = factor(outcome))) + geom_bar(stat = "identity",
show.legend = FALSE) + ggtitle("Probability Distribution", subtitle = "Outcome of a fair die") +
scale_x_continuous(breaks = 1:6) + scale_y_continuous(expand = c(0, 0), limits = c(0,
0.32)) + ylab("Expected probability") + bb_theme() + scale_fill_manual(values = banff()) +
theme(axis.ticks = element_blank())
df <- data.frame(Outcome = DieRoll(times = 6), NrRolls = 6)
one.roll <- ggplot(df, aes(x = Outcome, fill = factor(Outcome))) + geom_bar(aes(y = after_stat(count)/sum(count)),
show.legend = FALSE) + ggtitle("Proportions Observed", subtitle = "Outcome of a fair die\n(n = 6 trials)") +
scale_fill_manual(values = banff()) + scale_x_continuous(breaks = 1:12) + ylab(label = "Observed proportion") +
theme(axis.ticks = element_blank())
library(patchwork)
plot.one.dice.prob + one.rollIf we repeat die rolls a number of times, we can plot the proportions of {1,2,3,4,5,6} observed throughout many trials
What is the probability the sum of two dice is between six and eight?
plot.two.dice.prob <- data.frame(Outcome = factor(c(sapply(1:6, function(X) {
X + 1:6
})))) |>
ggplot(aes(x = Outcome)) + geom_bar(aes(y = after_stat(count)/sum(count)), group = 1,
show.legend = FALSE) + ggtitle("Probability Distribution", subtitle = "Outcome of the sum of two fair dice") +
scale_x_discrete(breaks = 1:12) + scale_y_continuous(expand = c(0, 0), limits = c(0,
0.2)) + ylab("Expected probability") + bb_theme() + theme(axis.ticks = element_blank())
plot.two.dice.prob\(P[6]+P[7]+P[8] - P[6 \text{ AND } 7 \text{ AND } 8]\)
data.frame(outcome = factor(c(2, 3, 4, 5, "6:8", 9, 10, 11, 12), levels = c(2, 3,
4, 5, "6:8", 9, 10, 11, 12)), prob = c(1, 2, 3, 4, 5 + 6 + 5, 4, 3, 2, 1)/36) |>
mutate(my.col = (outcome == "6:8")) |>
ggplot(aes(x = outcome, y = prob, fill = my.col)) + geom_bar(stat = "identity",
show.legend = FALSE) + ggtitle("Outcome of the sum of two fair dice") + scale_y_continuous(expand = c(0,
0), limits = c(0, 0.5)) + bb_theme() + ylab("Expected probability") + scale_fill_manual(values = c("lightgray",
"#006475")) + xlab(bquote(1^{
st
} ~ +~2^{
nd
} ~ roll)) + theme(axis.ticks = element_blank())The probability the sum of two dice is not between six and eight.
We know that \(\sum{P[X]}=1\), so \(P[\text{ not }X]=1-P[X]\)
dice7<-data.frame(outcome = factor(c("Not between 6 & 8", "Between 6 & 8"), levels = c("Not between 6 & 8", "Between 6 & 8")),prob = c((1+2+3+4+4+3+2+1) , (5 +6+5) ) / 36)
dice7 |>
mutate(my.col = (outcome == "6:8")) |>
ggplot(aes(x = outcome, y = prob, fill = outcome)) +
geom_bar(stat = "identity",show.legend = FALSE) +
ggtitle("Outcome of the sum of two fair dice") +
ylab("Expected probability") +
scale_fill_manual(values = c("lightgray","#006475")) +
scale_y_continuous(expand = c(0,0), limits = c(0,.7))+
bb_theme()+
xlab(bquote(1^{st}~+~2^{nd}~roll))+
theme(axis.ticks = element_blank())
Probability that the sum of two dice is odd or between 6 and 8.
Subtract P[A & B] to avoid double counting nonexclusive events
\(P[A \text{ or } B] = P[A] + P[B] - P[A \text{ and } B]\)
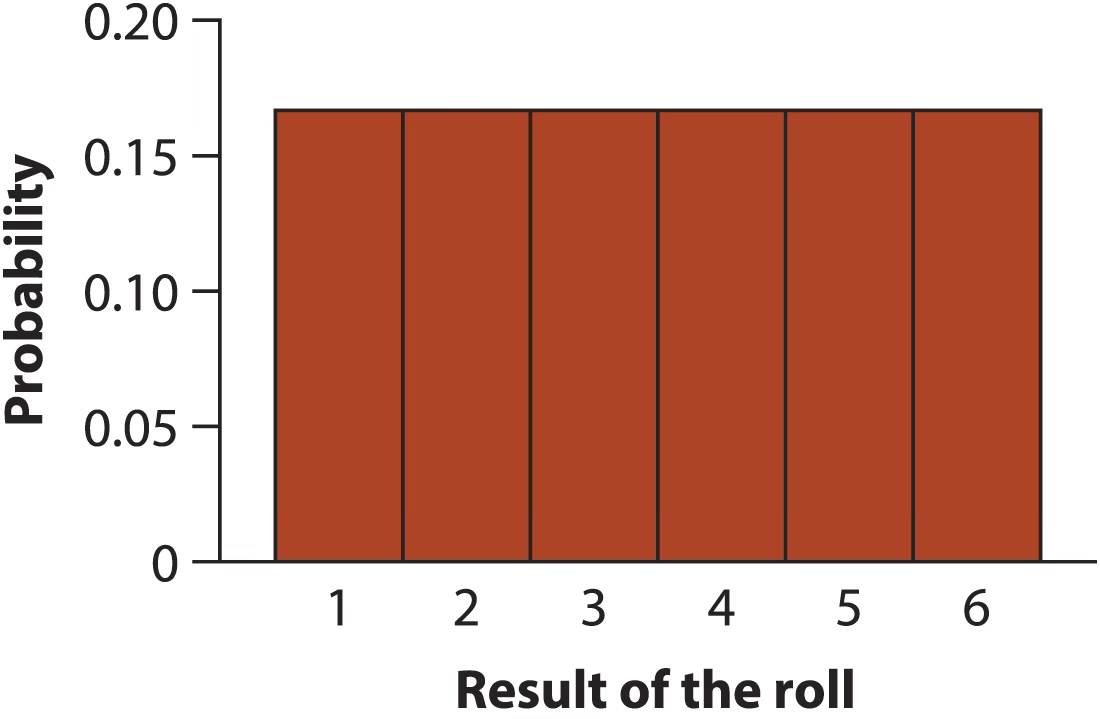
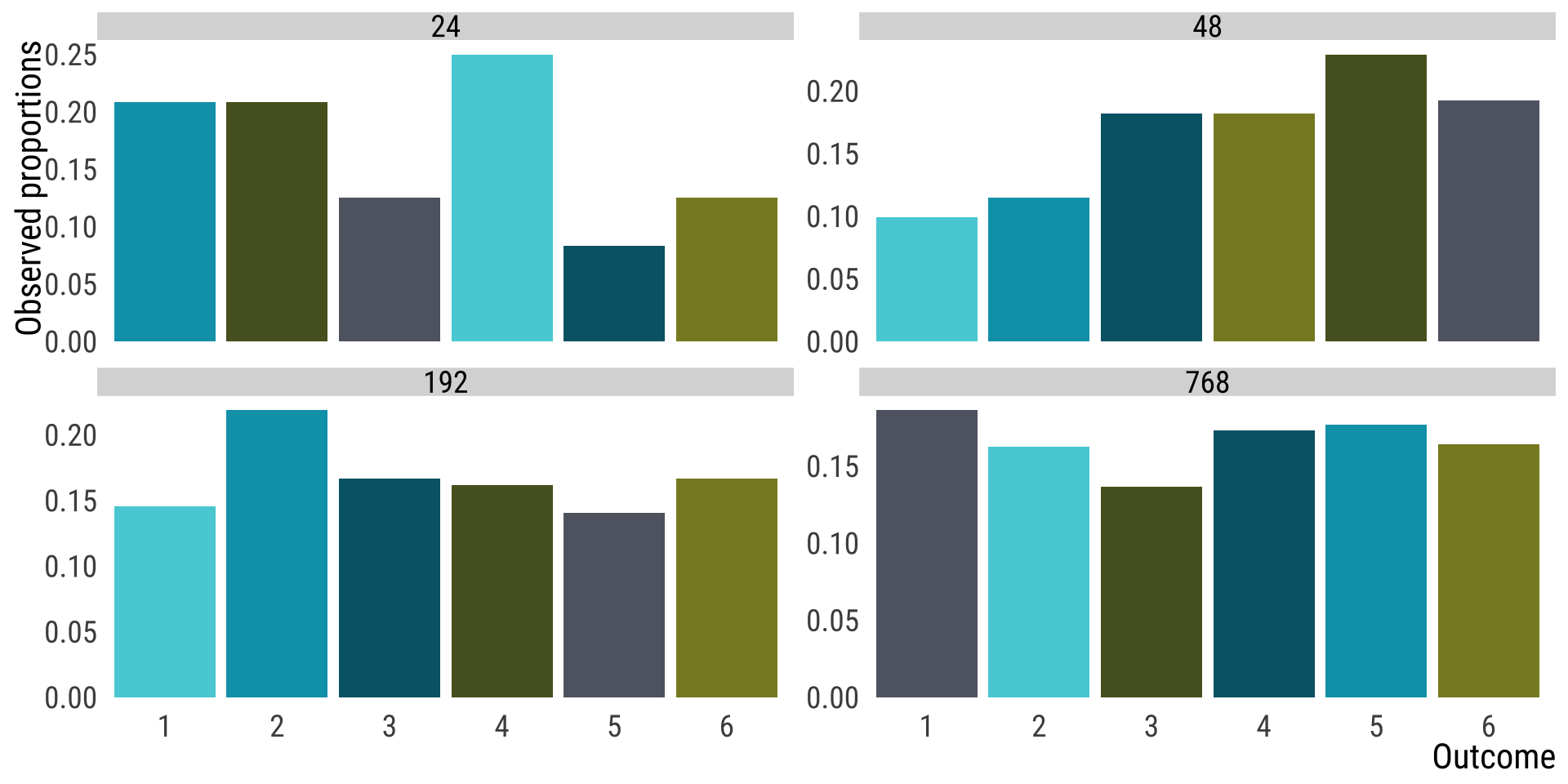
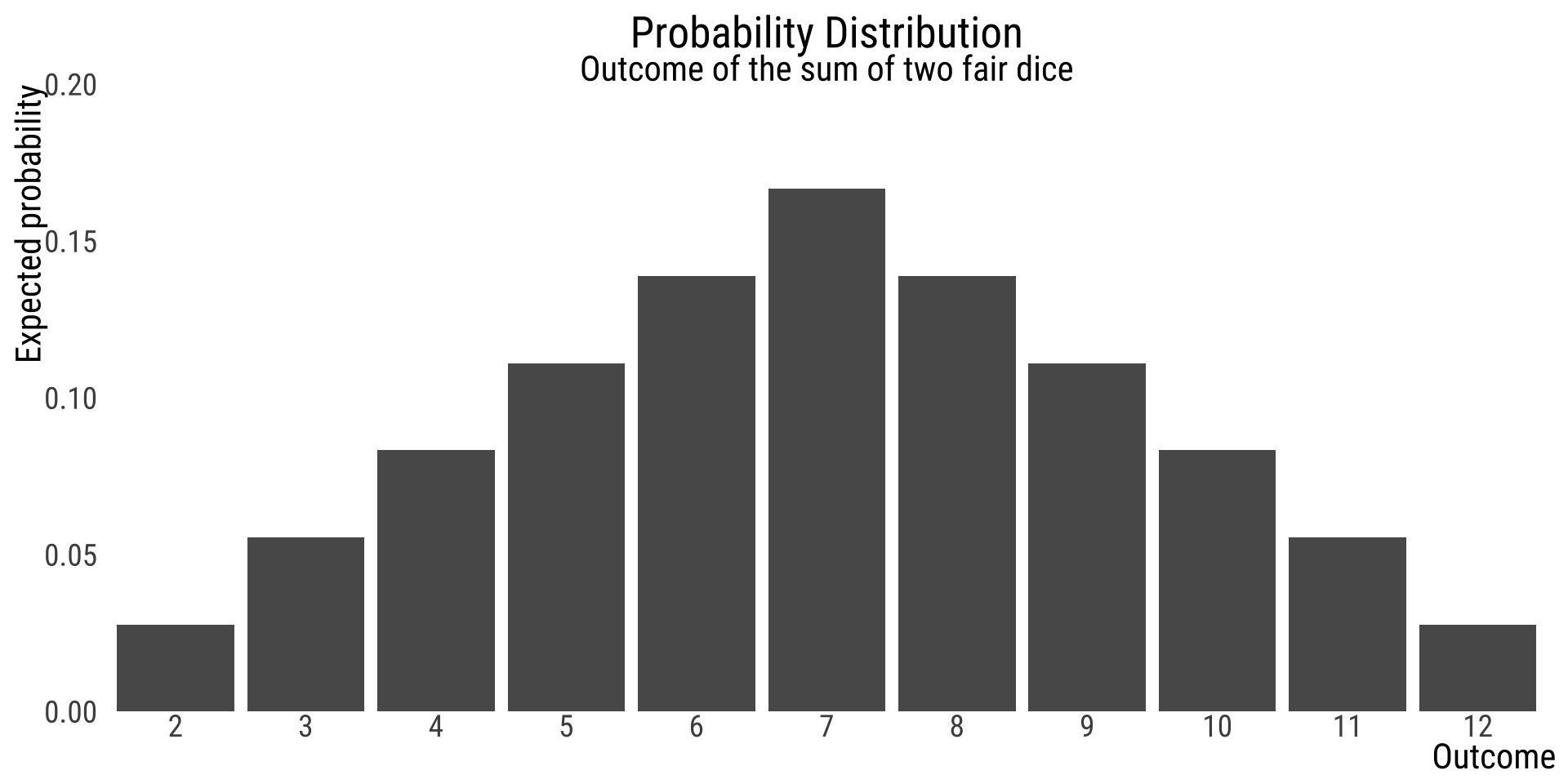
two.die.revisited <- data.frame(
Outcome = c(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12),
prob = c(1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1) / 36) |>
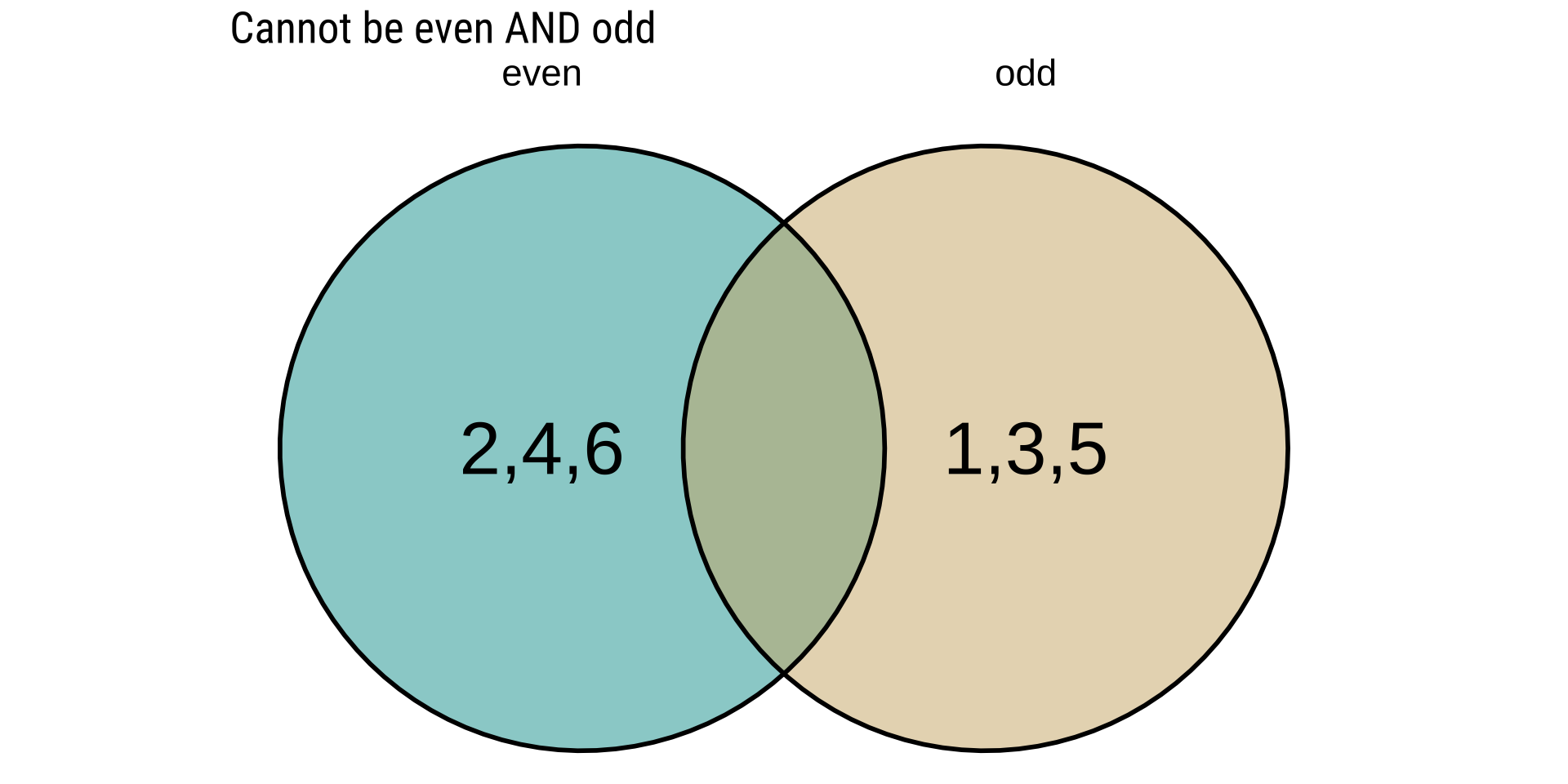
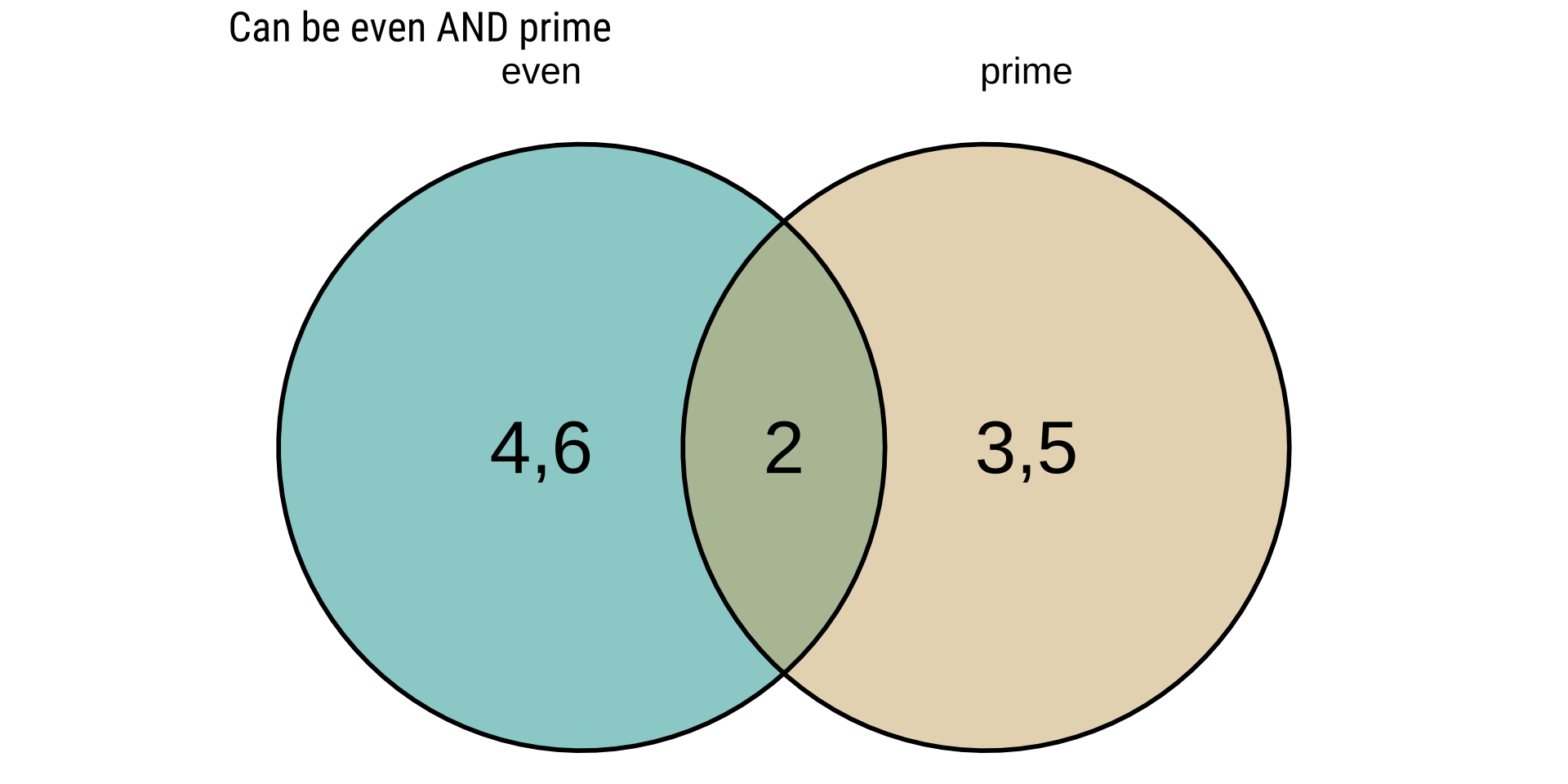
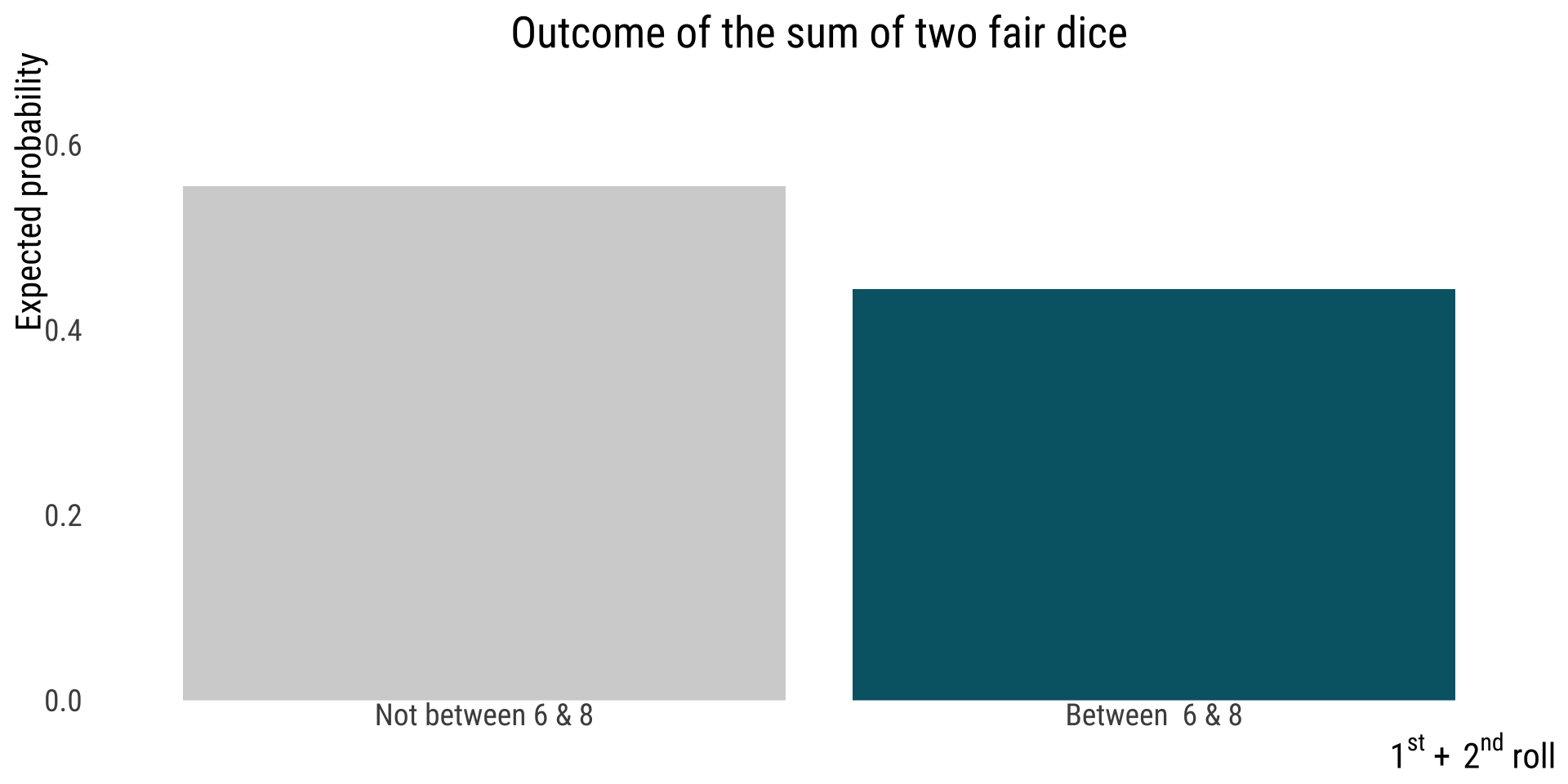
mutate(sixeight = Outcome >5 & Outcome <9,
odd = Outcome %%2 ==1,
oddandsixeight = sixeight & odd,
oddorsixeight = sixeight|odd)
dice.theme <- ggplot(two.die.revisited, aes(x = Outcome, y = prob)) +
ylab("")+
scale_y_continuous(expand = c(0,0), limits = c(0,.2))+
scale_x_continuous(breaks = 1:12) +
bb_theme() +
xlab(bquote(1^{st}~+~2^{nd}~roll))
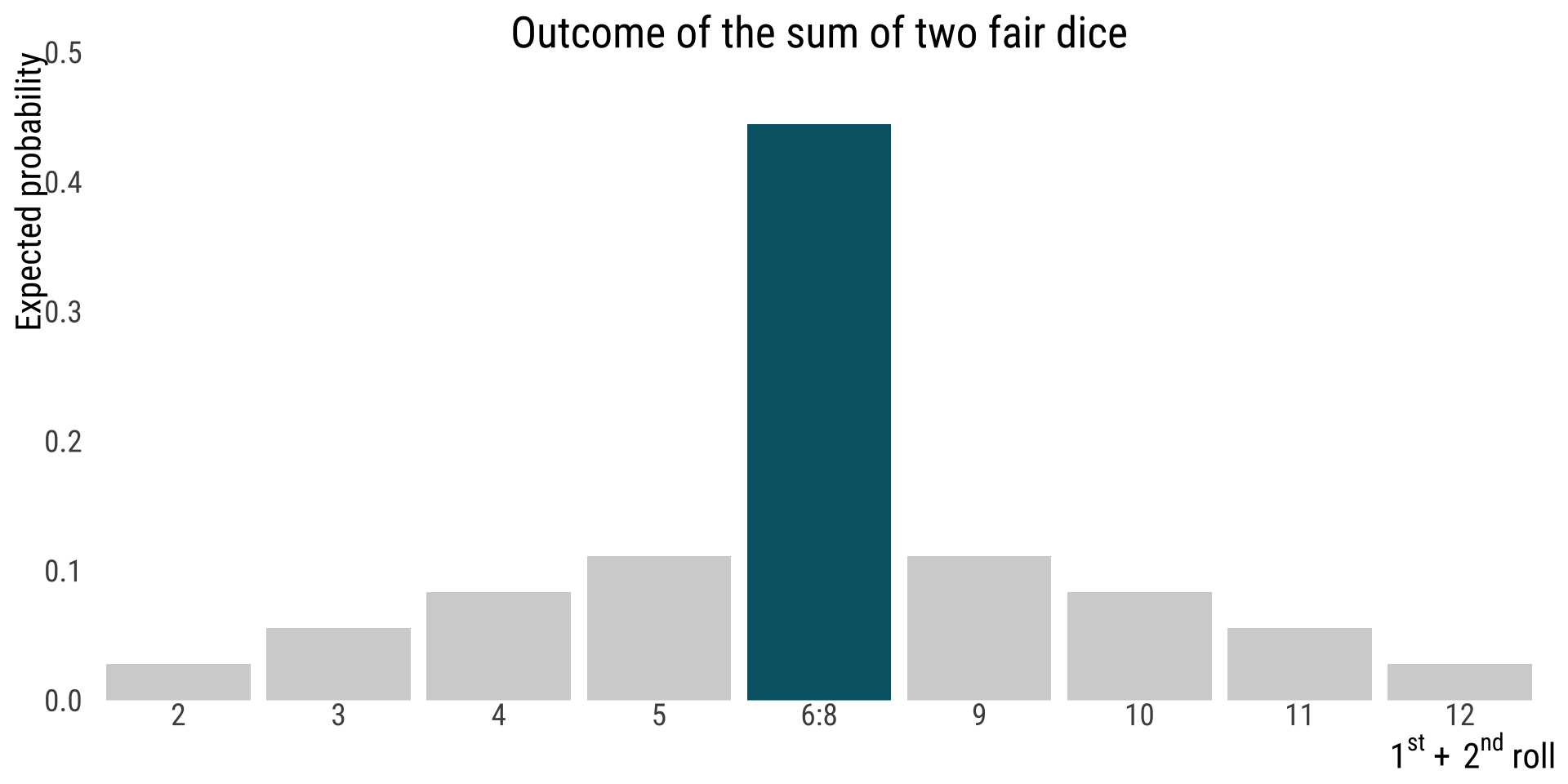
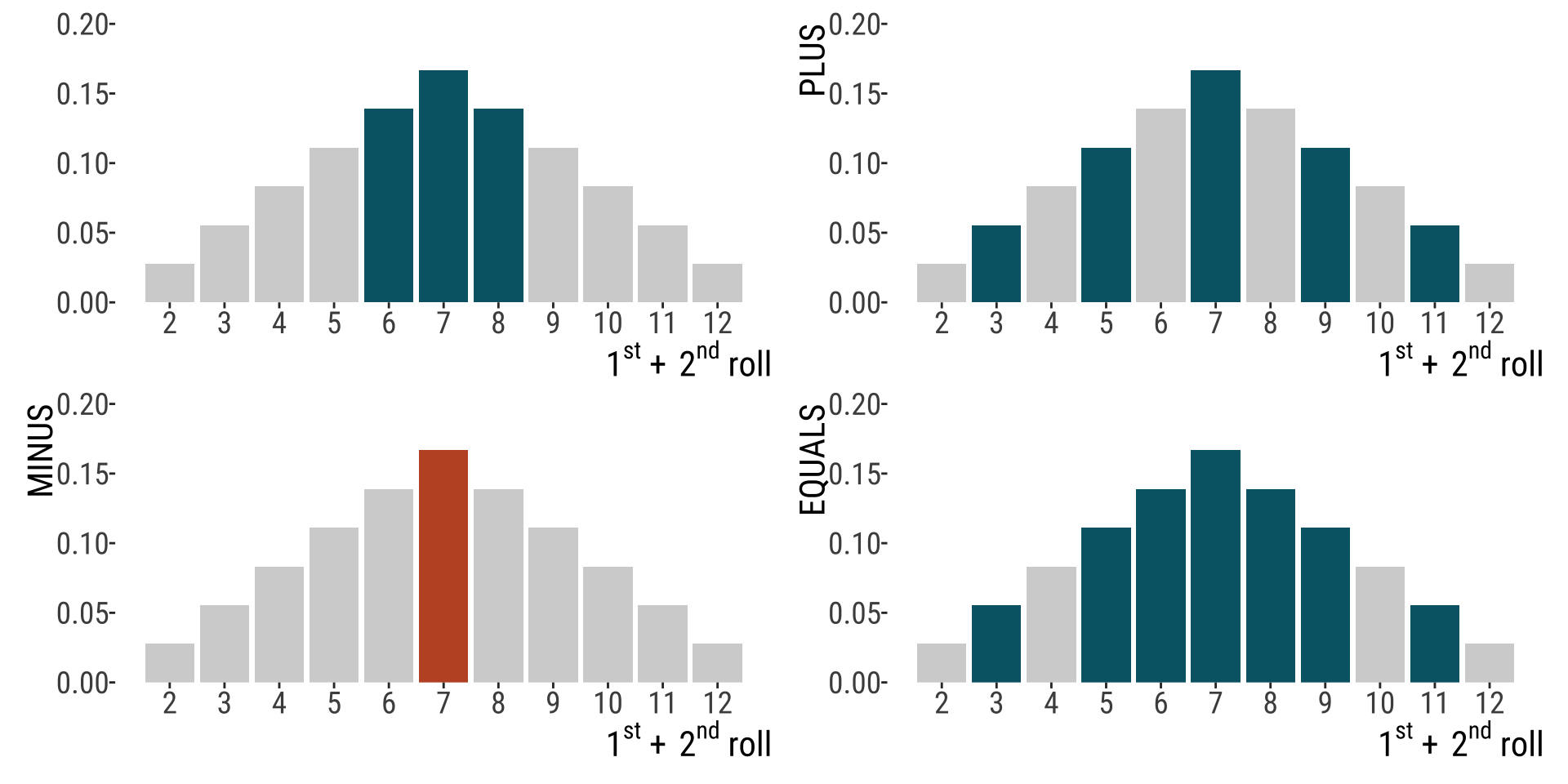
sixthrougheight <- dice.theme +
geom_bar(aes(fill = sixeight),stat = "identity",show.legend = FALSE) +
scale_fill_manual(values = c("lightgray","#006475"))
odd <- dice.theme +
geom_bar(aes(fill = odd),stat = "identity",show.legend = FALSE) +
scale_fill_manual(values = c("lightgray","#006475"))+
ylab("PLUS")
seven <- dice.theme +
geom_bar(aes(fill = oddandsixeight),stat = "identity",show.legend = FALSE) +
scale_fill_manual(values = c("lightgray","#C0532B"))+
ylab("MINUS")
tots <- dice.theme +
geom_bar(aes(fill = oddorsixeight),
stat = "identity",show.legend = FALSE) + scale_fill_manual(values = c("lightgray","#006475"))+
ylab("EQUALS")
library(patchwork)
sixthrougheight+ odd+ seven+ totsFrom: makeameme.org
